Предмет: Геометрия,
автор: kovalevichvadimm
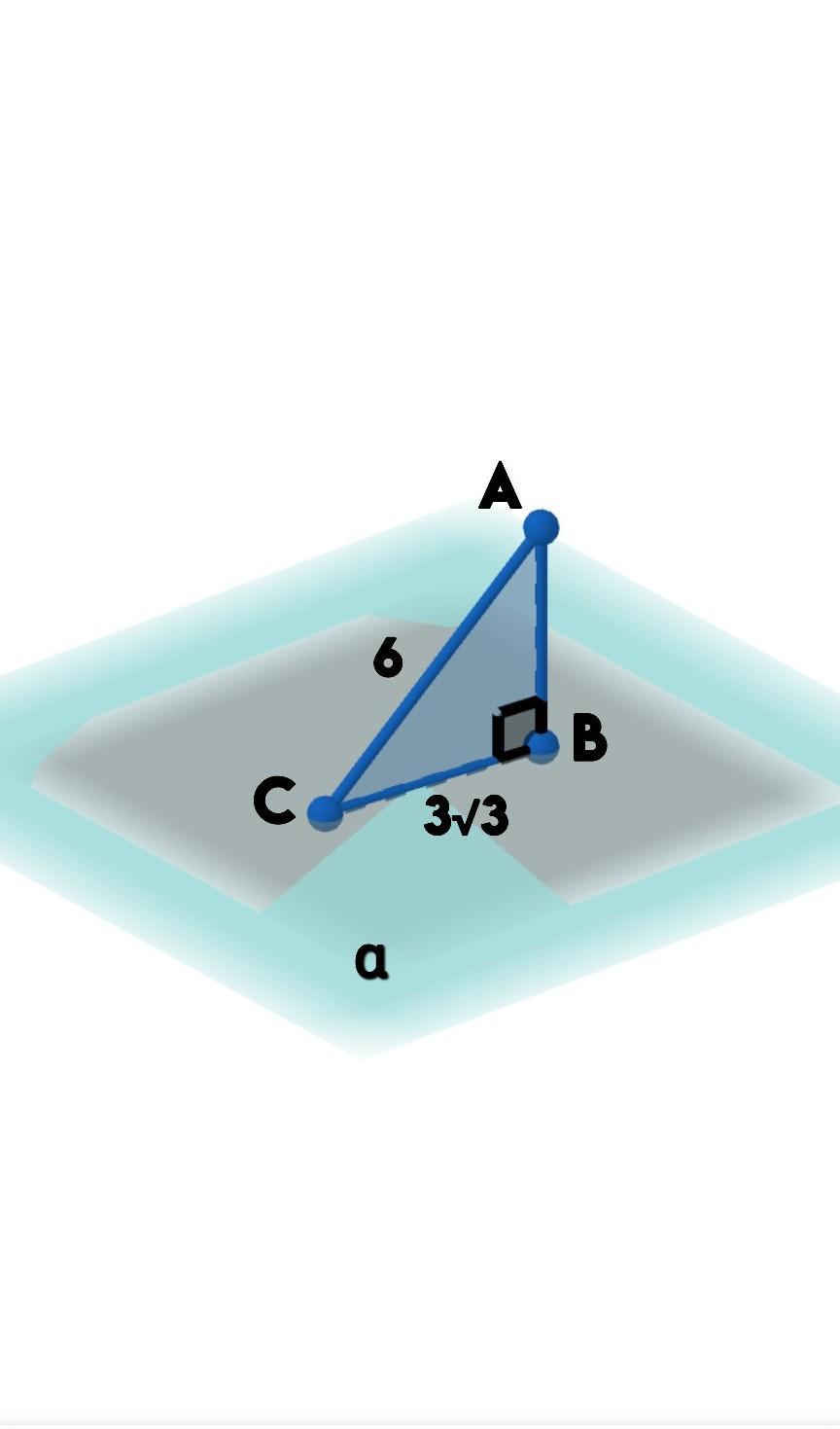
Знайти кут між прямою АС та площиною α, якщо СВ=3√3см, а АС= 6 см.
Ответы
Автор ответа:
6
Ответ:
∠(АС;α) = 30°
Объяснение:
ПЕРЕВОД: Найдите угол между прямой АС и плоскостью α, если СВ=3√3см, а АС= 6 см.
------------------------------------------------------
Дано: α - плоскость, ∆АВС, ∠В = 90°, СВ = 3√3см, АС = 6см
Найти: ∠(АС;α)
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Угол между прямой и плоскостью - это угол между прямой и ее проекцией на данную плоскость.
- Проекция наклонной АС это ВС. Искомый угол - ∠АСВ. Найдем его с помощью косинуса угла, которая равна отношению прилежащего катета(СВ) к гипотенузе(АС).
#SPJ1
Приложения:
Похожие вопросы
Предмет: Право,
автор: bezebala
Предмет: Математика,
автор: daniilmalahov98982
Предмет: Математика,
автор: nikitabatov100
Предмет: Математика,
автор: maryway2008
Предмет: Окружающий мир,
автор: ImLoveCoalas