Предмет: Математика,
автор: dasha29398
Знайдіть значення sin 2a, cos 2a, tg 2a ma tg a/2
Якщо вiдомо, щo:
Приложения:
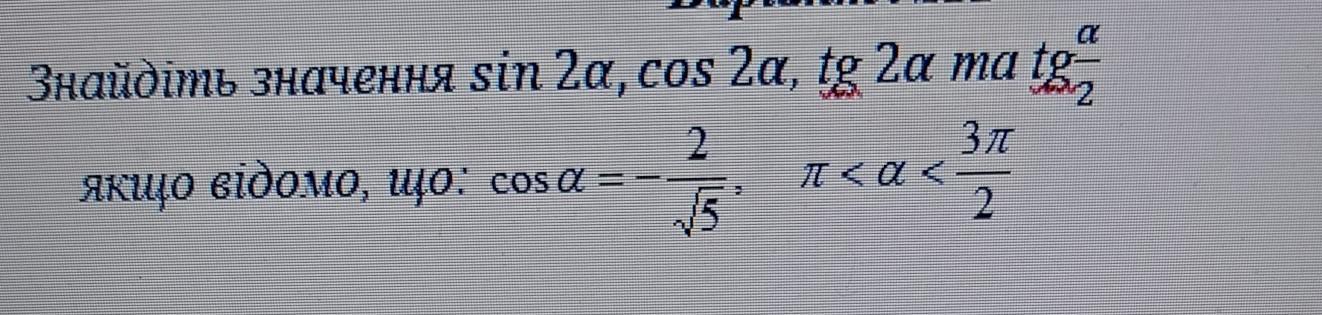
Ответы
Автор ответа:
3
Ответ:
Пошаговое объяснение:
Найти значения и
если известно , что
Найдем синус, используя основное тригонометрическое тождество:
Так как , то
угол третьей четверти , а синус в третьей четверти отрицательный
Найдем . Для этого воспользуемся формулой
Для нахождения воспользуемся формулой
Найдем . Для этого воспользуемся формулой
Найдем , используя формулу
#SPJ1
Похожие вопросы
Предмет: Алгебра,
автор: kuanysahmadiev2
Предмет: Українська література,
автор: anastasiiahridina201
Предмет: Обществознание,
автор: glnazmajlykl
Предмет: Литература,
автор: tasbulatovramil5667
Предмет: Русский язык,
автор: katehar