Question

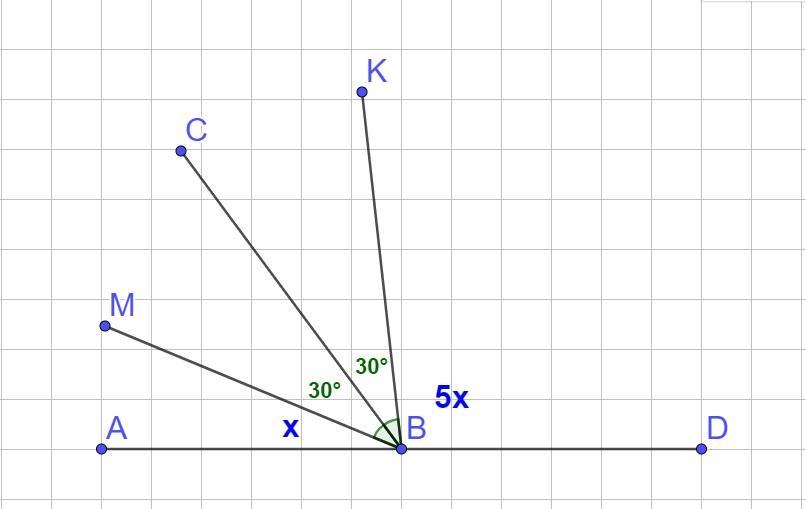
Кути АВС і DBC суміжні, промінь ВМ належить ку- ту АВС, промінь BK куту DBC, ZMBC = ZCBK = 30°, кут ДВК у 5 разів більший за кут АВМ. Знайдіть кути ABC i DBC.​ помогите пожалуйста

Answer 1

Ответ:

∠АВС=50°;  ∠DBC=130°

Объяснение:

Кути АВС і DBC - суміжні, промінь ВМ належить ∠АВС, промінь BK ∠DBC, ∠MBC = ∠CBK = 30°, ∠DВК у 5 разів більший за ∠АВМ. Знайдіть кути ABC i DBC.​

• Два кути називають суміжними, якщо в них одна сторона спільна, а дві інші є доповняльними променями

• Сума суміжних кутів дорівнює 180°.

• Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

Нехай х– коефіцієнт пропорційності, тоді ∠АВМ=х, ∠DВК= 5х.

∠АВС і ∠DBC є суміжними. За теоремою: сума суміжних кутів дорівнює 180° маємо:

∠АВС + ∠DBC = 180°

∠АВС=∠АВМ+∠MBC;  ∠DBC=∠СВК+∠DВК.

За умовою ∠MBC = ∠CBK = 30°.

Маємо рівняння:

х+30°+30°+5х=180°

6х=180°-60°

6х=120°

х=20°

Тоді ∠АВМ=20°, ∠DВК= 5х=5·20°=100°.

Отже: ∠АВС=20°+30°=50°;  ∠DBC=30°+100°=130°.

Відповідь: ∠АВС=50°;  ∠DBC=130°.

#SPJ1