Предмет: Алгебра,
автор: Aaaaaaaaalisaaaaaaaa
1. Дана функция f (x) =-x²+4x-4 ) Найдите критические точки функции. а) Определите промежутки монотонности. c) Запишите уравнение асимптот функции. Используя результаты задания 1, постройте схематически график функции
даю 20 баллов, кто ответит фигню - блок и жалоба. помогите, пожалуйста
Приложения:

Ответы
Автор ответа:
2
а) Критические точки функции - это точки, в которых производная функции равна нулю или не существует. Для функции f(x) = -x² + 4x - 4 производная равна f'(x) = -2x + 4.
Решим уравнение -2x + 4 = 0:
-2x = -4
x = 2
Таким чином, критическая точка функции f(x) - это точка x = 2.
б) Для определения промежутков монотонности нужно проанализировать знак производной функции на каждом интервале между критическими точками и на крайних интервалах.
Критическая точка x = 2 делит ось абсцисс на два интервала: (-∞, 2) и (2, +∞).
На интервале (-∞, 2) производная f'(x) < 0, тобто функция f(x) монотонно убывает.
На интервале (2, +∞) производная f'(x) > 0, тобто функция f(x) монотонно возрастает.
в) Для пошуку асимптот необхідно розглянути границі функції при x -> ±∞.
При x -> ±∞, -x² стає набагато більш значущим, ніж 4x та -4. Тому можна приблизно записати функцію у вигляді f(x) ≈ -x².
Якщо поділити функцію на x при x -> ±∞, отримаємо відповідно дві асимптоти: y = -x та y = -x + 4.
г) Схематичний графік функції f(x) = -x² + 4x - 4:
На графіку зображені критичні точки x = 2, асимптоти y = -x та y = -x + 4, а також напрямки монотонності на різних інтервалах.
Решим уравнение -2x + 4 = 0:
-2x = -4
x = 2
Таким чином, критическая точка функции f(x) - это точка x = 2.
б) Для определения промежутков монотонности нужно проанализировать знак производной функции на каждом интервале между критическими точками и на крайних интервалах.
Критическая точка x = 2 делит ось абсцисс на два интервала: (-∞, 2) и (2, +∞).
На интервале (-∞, 2) производная f'(x) < 0, тобто функция f(x) монотонно убывает.
На интервале (2, +∞) производная f'(x) > 0, тобто функция f(x) монотонно возрастает.
в) Для пошуку асимптот необхідно розглянути границі функції при x -> ±∞.
При x -> ±∞, -x² стає набагато більш значущим, ніж 4x та -4. Тому можна приблизно записати функцію у вигляді f(x) ≈ -x².
Якщо поділити функцію на x при x -> ±∞, отримаємо відповідно дві асимптоти: y = -x та y = -x + 4.
г) Схематичний графік функції f(x) = -x² + 4x - 4:
На графіку зображені критичні точки x = 2, асимптоти y = -x та y = -x + 4, а також напрямки монотонності на різних інтервалах.
Приложения:
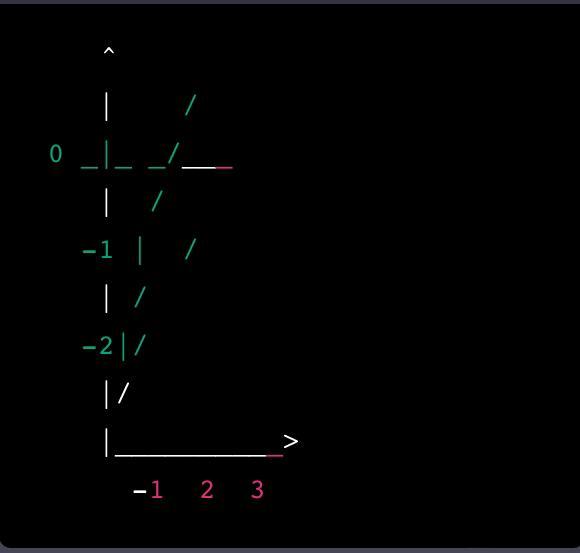
Aaaaaaaaalisaaaaaaaa:
спасибо большое ❤
Похожие вопросы
Предмет: Математика,
автор: andrianaosipko0
Предмет: Геометрия,
автор: ajaru6311
Предмет: Русский язык,
автор: altosha108
Предмет: Математика,
автор: avdeevalera08