Срочно помогите ОЧЕНЬ НАДО
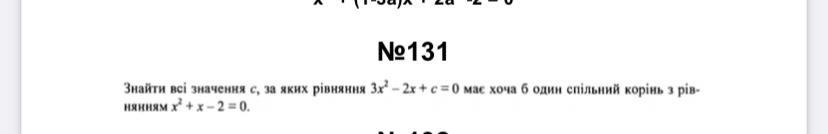

Ответы
Відповідь:
Пояснення:
Спочатку знайдемо корені рівняння x^2 + x - 2 = 0:
Для цього скористаємось формулою дискримінанту:
D = b^2 - 4ac, де a = 1, b = 1, c = -2
D = 1^2 - 4(1)(-2) = 9
Корені рівняння знаходяться за формулою:
x1,2 = (-b ± √D) / 2a
x1 = (-1 + √9) / 2 = 1
x2 = (-1 - √9) / 2 = -2
Тепер, щоб знайти значення c, за яких рівняння 3x^2 - 2x + с = 0 має хоча б один спільний корінь з рівнянням x^2 + x - 2 = 0, потрібно, щоб і три корені 3x^2 - 2x + с = 0 співпадали з коренями рівняння x^2 + x - 2 = 0.
Знайдемо значення с, які виконують цю умову:
Для цього спочатку знайдемо корені рівняння 3x^2 - 2x + с = 0:
x1,2 = (-b ± √D) / 2a, де a = 3, b = -2, c = с
D = (-2)^2 - 4(3)(с) = 4 - 12с
Якщо рівняння має хоча б один спільний корінь з x^2 + x - 2 = 0, то один з коренів рівняння 3x^2 - 2x + с = 0 повинен бути рівний 1, або -2.
Коли x1 = 1:
3(1)^2 - 2(1) + с = 0
3 - 2 + с = 0
с = -1
Коли x1 = -2:
3(-2)^2 - 2(-2) + с = 0
12 + 4 + с = 0
с = -16
Отже, рівняння 3x^2 - 2x - 1 = 0 та 3x^2 - 2x - 16 = 0 мають хоча б один спільний корінь з рівнянням x^2 + x - 2 = 0 при c = -1 та c = -16 відповідно.