Предмет: Математика,
автор: agent0000788
Терміново допоможіть з завданням
Приложения:
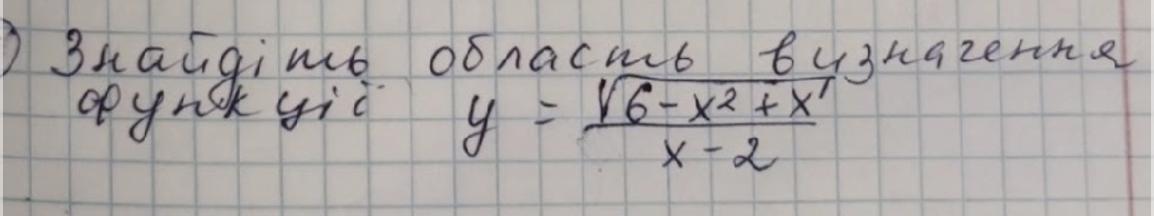
Ответы
Автор ответа:
0
Ответ:
Подкоренное выражение должно быть неотрицательным, а знаменатель не может равняться 0 .
Приложения:
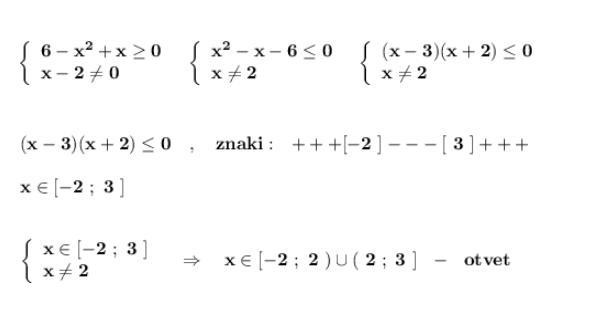
Похожие вопросы
Предмет: Химия,
автор: olareznik246
Предмет: Алгебра,
автор: yasheritza0711
Предмет: Английский язык,
автор: Cvetochek09
Предмет: Другие предметы,
автор: Аноним