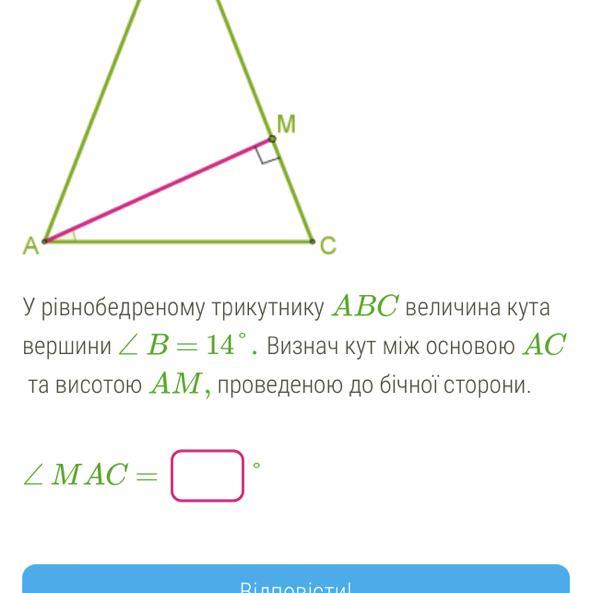
У рівнобедреному трикутнику ABC величина кута
-
вершини Z B = 14°. Визнач кут між основою АС
та висотою АМ, проведеною до бічної сторони.
Ответы
Відповідь:
Пояснення:
Оскільки трикутник ABC є рівнобедреним, то кути при основі АС також будуть рівними. Позначимо ці кути як x. Також зазначено, що кут вершини ZB дорівнює 14°.
Тоді сума кутів при вершинах трикутника ABC дорівнює 180°, тому:
2x + 14° + 90° = 180°
2x = 76°
x = 38°
Отже, кути при основі трикутника ABC дорівнюють 38° кожен.
Далі, позначимо кут між основою АС і висотою АМ як y. За властивостями рівнобедреного трикутника, висота АМ є медіаною і бісектрисою бічної сторони, тому кут між висотою АМ і бічною стороною, дорівнює половині кута при вершині B, тобто 7°.
Застосовуючи теорему про суму кутів в трикутнику, маємо:
x + y + 7° = 180°
Замінюємо виразом для x та розв'язуємо рівняння:
38° + y + 7° = 180°
y = 135°
Отже, кут між основою АС та висотою АМ дорівнює 135°.