1) (4a³ - 1) (9a³+5)-(6a³-1)² 3) (d − 3) (d' + 7) − (ď + 2)² - 2) (c² − 1)² − (cª + 4) (cª − 6) 4) (k³ + 9) (11 − k³) + (k³ + 1)² -
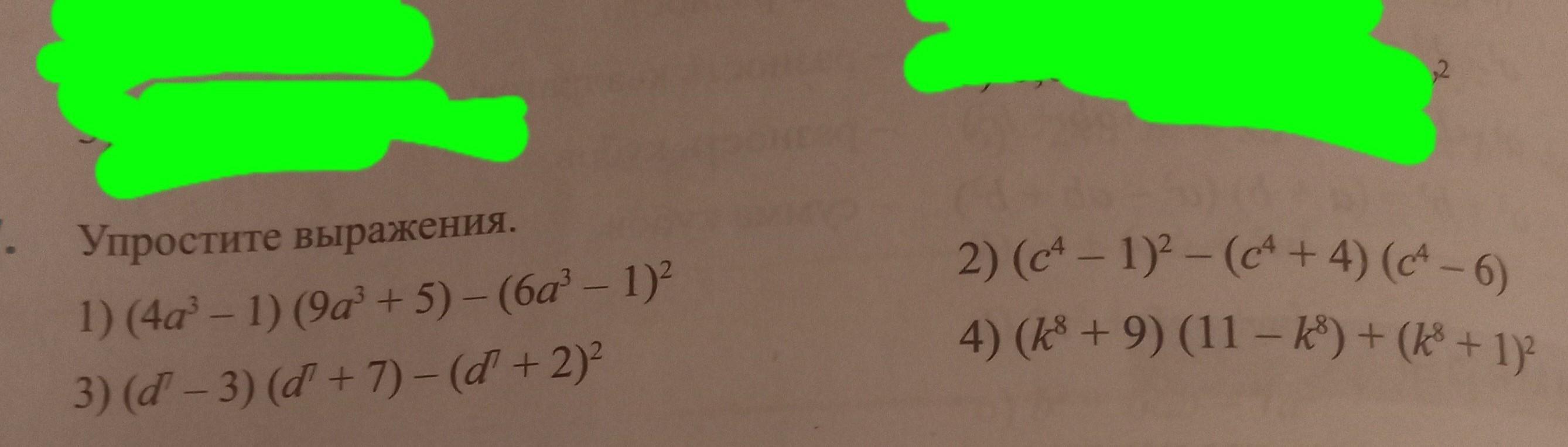
Ответы
1)Для розв'язання цього прикладу потрібно розкрити дужки та спростити вираз:
(4a³ - 1) (9a³+5) - (6a³ - 1)² = (36a^6 + 20a^3 - 9a^3 - 5) - (36a^6 - 12a^3 + 1)
= 36a^6 + 20a^3 - 9a^3 - 5 - 36a^6 + 12a^3 - 1
= 23a^3 - 6
Таким чином, вираз (4a³ - 1) (9a³+5)-(6a³-1)² дорівнює 23a^3 - 6.
2)Почнемо з розкриття дужок в першому доданку:
(c⁴-1)² = c⁸ - 2c⁴ + 1
Теперішній вираз виглядає так:
(c⁸ - 2c⁴ + 1) - (c⁸ - 10c⁴ - 24)
Розкриваємо дужки в другому доданку:
(c⁴+4)(c⁴-6) = c⁸ - 2c⁴ - 24
Підставляємо це вираз у вихідний:
(c⁸ - 2c⁴ + 1) - (c⁸ - 2c⁴ - 24)
Віднімаємо вирази у дужках:
c⁸ - 2c⁴ + 1 - c⁸ + 2c⁴ + 24
Зводимо подібні доданки:
26
Таким чином, (c⁴-1)²-(c⁴+4)(c⁴-6) = 26.
3)Почнемо з розкриття дужок в першому добутку:
(d⁷-3)(d⁷+7) = d¹⁴ + 4d⁷ - 21
Теперішній вираз виглядає так:
(d¹⁴ + 4d⁷ - 21) - (d¹⁴ + 4d⁷ + 4)
Розкриваємо дужки в другому доданку:
(d⁷+2)² = d¹⁴ + 4d⁷ + 4
Підставляємо це вираз у вихідний:
(d¹⁴ + 4d⁷ - 21) - (d¹⁴ + 4d⁷ + 4)
Віднімаємо вирази у дужках:
d¹⁴ + 4d⁷ - 21 - d¹⁴ - 4d⁷ - 4
Зводимо подібні доданки:
-25
Таким чином, (d⁷-3)(d⁷+7)-(d⁷+2)² = -25.