Предмет: Алгебра,
автор: lizaasulinskayy
Помогите решить пример ( Обчисліть визначений інтеграл )
Приложения:
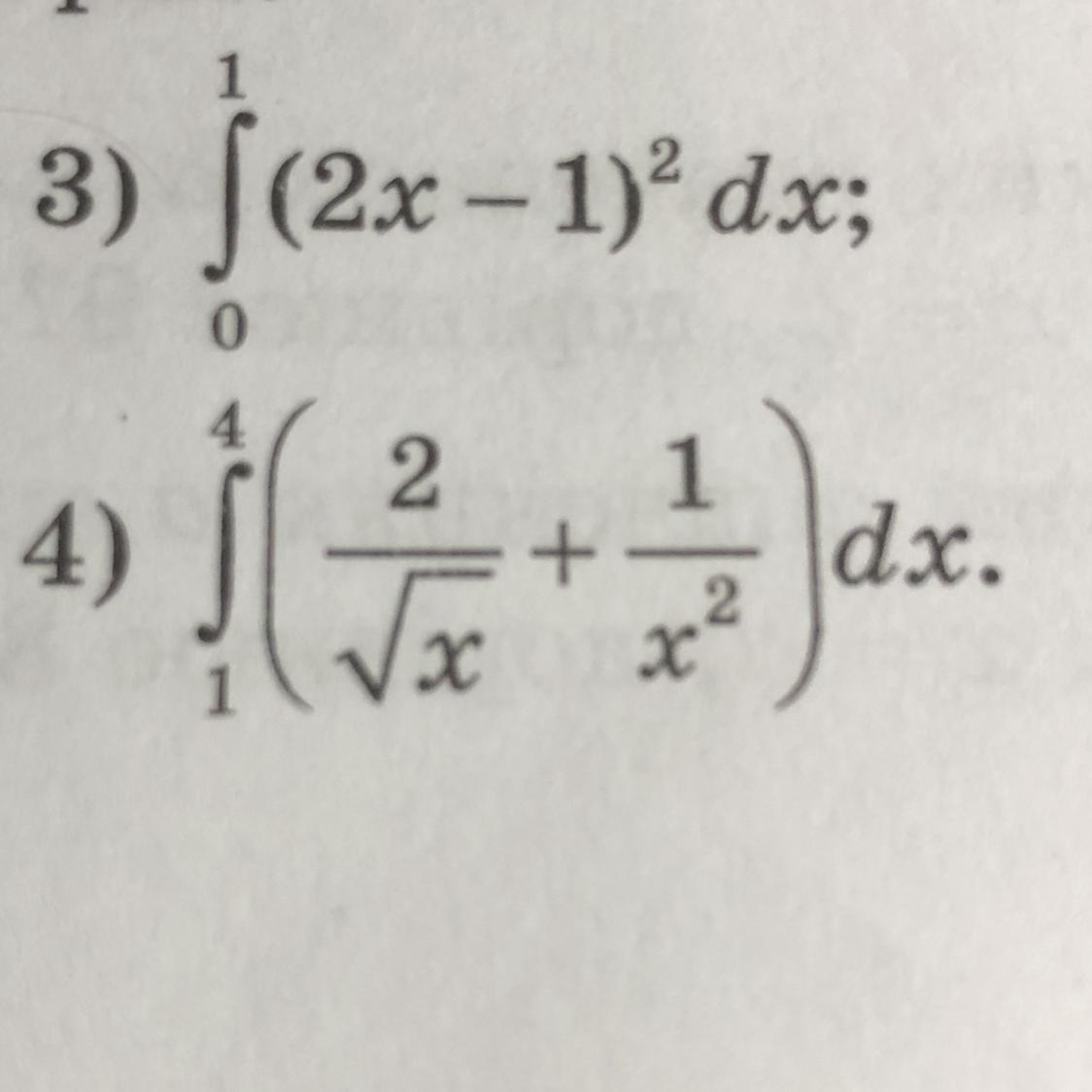
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Вычислить интеграл:
- Интеграл степенной функции:
- Формула Ньютона- Лейбница:
Похожие вопросы
Предмет: Английский язык,
автор: nika92675
Предмет: Алгебра,
автор: skater01
Предмет: Физика,
автор: standoffstandoffer92
Предмет: Астрономия,
автор: sanycs444
Предмет: Музыка,
автор: romamoiseev721