ПОМОГИТЕ, ПОЖАЛУЙСТА!!!! СРОЧНО!!!!
ДАЮ ВСЕ БАЛЛЫ, ЧТО У МЕНЯ ЕСТЬ :(((
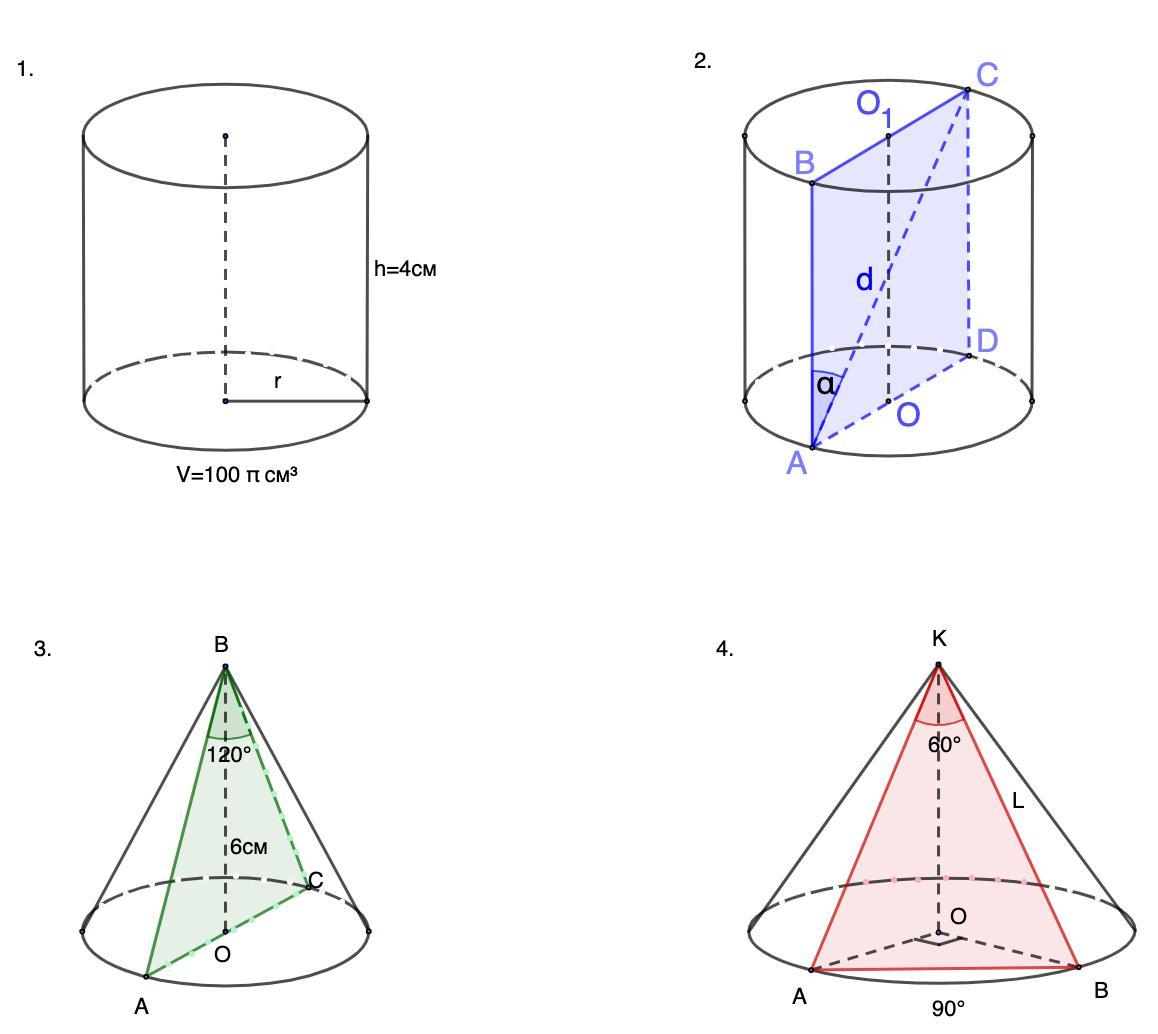
1. Об'єм циліндра дорівнює 100п см3. Знайдіть площу повної поверхні циліндра, якщо його висота дорівнює 4 см.
2. Діагональ осьового перерізу циліндра дорівнює d і утворює з твірною циліндра кут а (альфа). Знайдіть площу бічної поверхні циліндра.
3. Висота конуса дорівнює 6 см, а кут при вершині осьового перерізу - 120°. Знайдіть площу бічної поверхні конуса.
4. Через вершину конуса проведено площину, що перетинає основу по хорді, яка стягує дугу 90°. Знайдіть площу повної поверхні конуса, якщо його твірна дорівнює L, а кут у перерізі при вершині конуса - 60°.
Ответы
Ответ:
1. Площадь полной поверхности цилиндра равна 90π см².
2. Площадь боковой поверхности цилиндра равна πd²sinα cosα.
3. Площадь боковой поверхности конуса равна 72√3π см².
4. Площадь полной поверхности конуса равна ед.²
Объяснение:
1. Объем цилиндра равен 100π см³. Найдите площадь полной поверхности цилиндра, если его высота равна 4 см.
2. Диагональ осевого сечения цилиндра равна d и образует с образующей цилиндра угол α. Найдите площадь боковой поверхности цилиндра.
3. Высота конуса равна 6 см, а угол при вершине осевого сечения - 120°. Найдите площадь боковой поверхности конуса.
4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, которая стягивает дугу 90°. Найдите площадь полной поверхности конуса, если его образующая равна L, а угол в сечении при вершине конуса - 60°.
1. Дано: цилиндр;
Vц = 100π см³;
h = 4 см.
Найти: Sполн.
Решение:
- Площадь полной поверхности найдем по формуле:
Sполн. = 2Sосн. + Sбок.
- Объем цилиндра равен:
V = πr²h,
где r - радиус основания; h - высота цилиндра.
V = 100π см; h = 4 см
100π = πr² · 4 ⇒ r² = 25 ⇒ r = 5 см
- Площадь боковой поверхности равна:
Sбок. = 2πrh
Sбок. = 2π · 5 · 4 = 40π (см²)
- Площадь основания равна:
Sосн. = πr²
Sосн. = 25π см²
⇒ Sполн. = 2 · 25π + 40π = 90π (см²)
Площадь полной поверхности цилиндра равна 90π см².
2. Дано: цилиндр;
ABCD - осевое сечение;
АС = d; ∠BAC = α.
Найти: Sбок.
Решение:
- Площадь боковой поверхности цилиндра равна:
Sбок. = 2πrh,
где r - радиус основания; h - высота цилиндра.
Найдем r и h.
Рассмотрим ΔАВС - прямоугольный.
АС = d; ∠BAC = α.
- Синус угла - отношение противолежащего катета к гипотенузе.
ВС = 2r - диаметр основания цилиндра.
- Косинус угла - отношение прилежащего катета к гипотенузе.
AB = h - высота цилиндра.
⇒ Sбок. = 2πrh = π · d · sinα · d · cosα = πd²sinα cosα
Площадь боковой поверхности цилиндра равна πd²sinα cosα.
3. Дано: конус;
АВС - осевое сечение;
ВО = 6 см - высота конуса;
∠АВС = 120°.
Найти: Sбок.
Решение:
- Площадь боковой поверхности конуса равна:
Sбок. = πrl,
где r - радиус основания; l - образующая конуса.
Рассмотрим ΔАВС - равнобедренный.
- В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой.
⇒ ∠ОВС = 120° : 2 = 60°
Рассмотрим ΔОВС - прямоугольный.
- Тангенс угла - отношение противолежащего катета к прилежащему.
Найдем l:
⇒ Sбок. = πrl = π · 6√3 · 12 = 72√3 π (см²)
Площадь боковой поверхности конуса равна 72√3π см².
4. Дано: конус;
АКВ - сечение;
◡АВ = 90°;
КВ = L; ∠АКВ = 60°
Найти: Sполн.
Решение:
- Площадь полной поверхности конуса найдем по формуле:
Sполн. = πrl + πr²,
где r - радиус основания; l - образующая конуса.
Рассмотрим ΔАКВ - равнобедренный.
∠АКВ = 60°.
- Если в равнобедренном треугольнике есть угол 60°, то он равносторонний.
⇒ АК = КВ = АВ = L
Рассмотрим ΔАОВ - равнобедренный (АО = ОВ = R).
- Центральный угол измеряется градусной мерой дуги, на которую он опирается.
⇒ ∠АОВ = ◡АВ = 90°
ΔАОВ - равнобедренный, прямоугольный.
По теореме Пифагора найдем R:
AB² = AO² + OB²
L² = 2R² ⇒ R = L/√2
Sполн. = πrl + πr² =
Площадь полной поверхности конуса равна ед.²
#SPJ1