Предмет: Геометрия,
автор: onopriakmaks
Сторона трикутника 21 см, а дві інші утворюють між собою кут 60 відносяться як 8:3. Знайдіть периметр трикутника.
Ответы
Автор ответа:
8
Ответ:
54 см
Объяснение:
Сторона треугольника равна 21 см, а две другие образуют между собой угол 60° и относятся как 8:3 . Найти периметр треугольника.
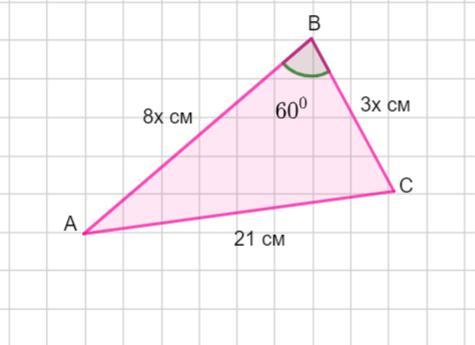
Пусть дан ΔАВС. Сторона АС = 21 см, АВ : ВС =8:3 . ∠АВС =60°.
Периметр треугольника - это сумма длин всех сторон .
Найдем стороны треугольника. Пусть АВ = 8х см, а ВС =3х см. Тогда к данному треугольнику применим теорему косинусов:
квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Так как стороны треугольника определяются положительными числами , то х= 3 и тогда найдем стороны треугольника
см
см.
Тогда периметр
Значит, периметр треугольника равен 54 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: bogdanazaremska7
Предмет: Информатика,
автор: nailbagirov44
Предмет: Українська мова,
автор: pavelromashkow
Предмет: Математика,
автор: nastaolejnik2626
Предмет: Литература,
автор: vietrung3018