Question

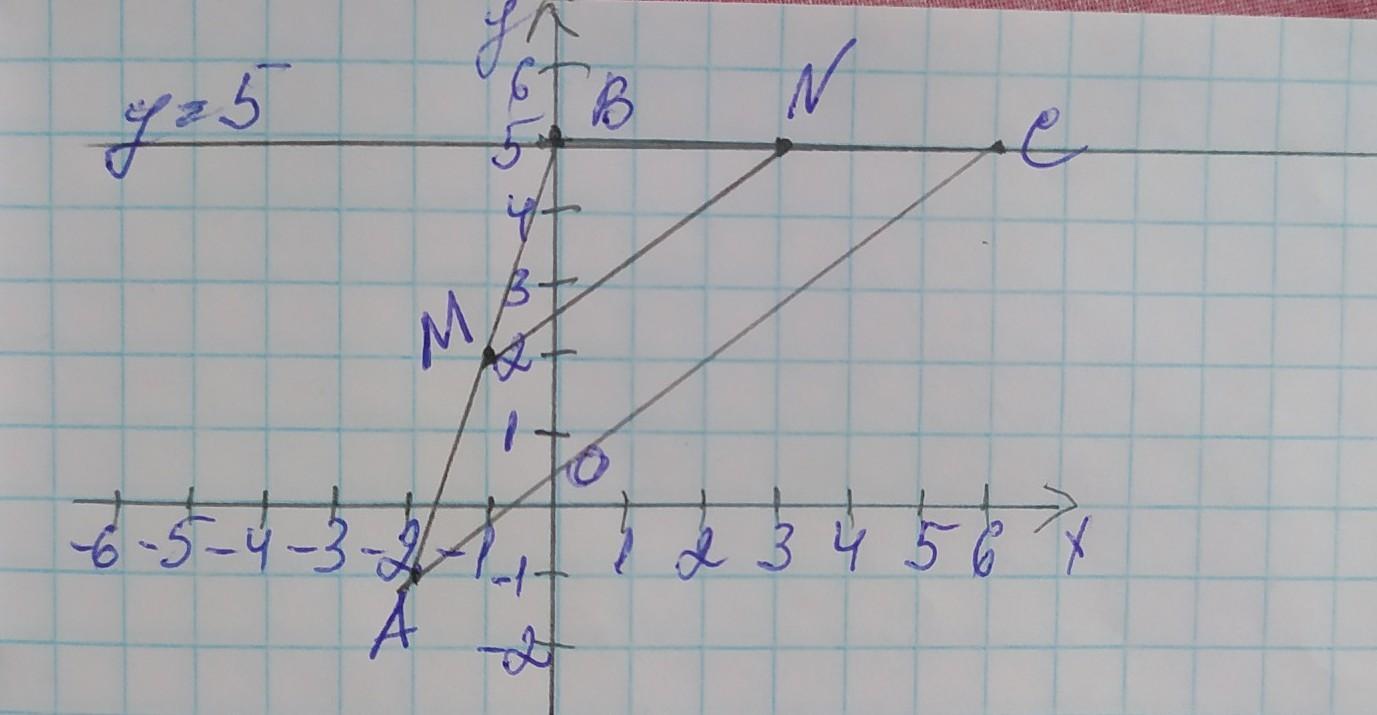
Дано точки А(-2;-1), B(0;5), C(6;5). MN середня лінія трикутника ABC, MN||AC, Me AB.
а) Знайдіть координати точки М.

б) Знайдіть довжину MN.

В) Визначте, які з точок А, В, С, М, И належать прямій y=5.

Answer 1

Ответ:

a) M(–1; 2)

б) MN=5

в) B, C, N

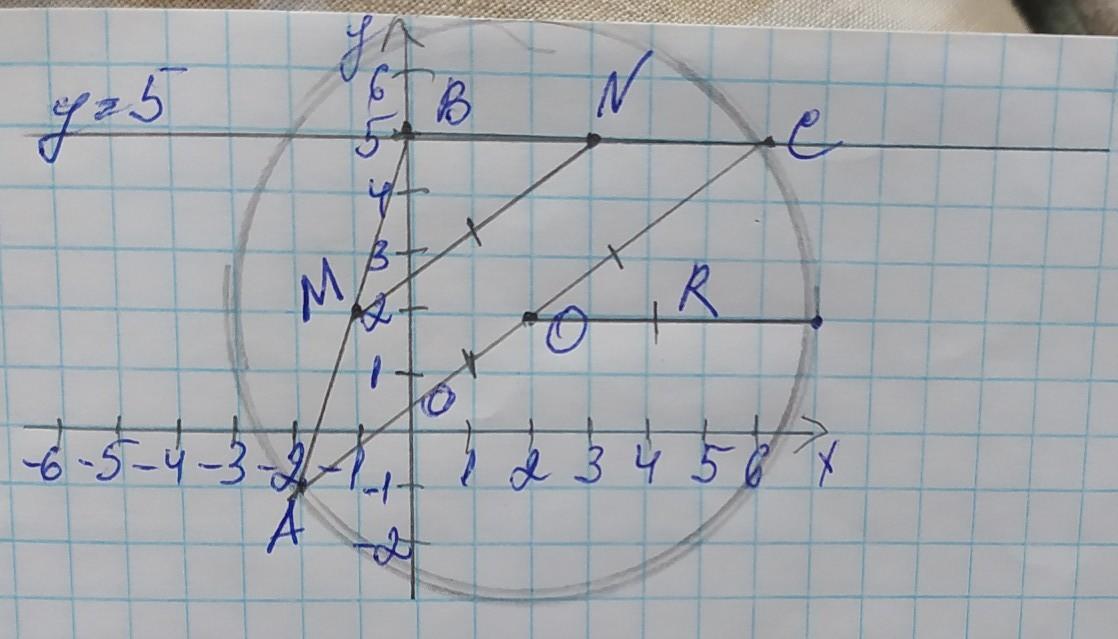
г) (х–2)²+(у–2)²=25

Объяснение:

ДАНО:

∆АВС; А(–2; –1); В(0; 5); С(6; 5); МN – середня лінія ∆АВС; MN || AC; M ∈ AB; пряма у=5

ЗНАЙТИ:

а) координати точки M;

б) довжину МN

в) яки з точок А, В, С, М, N належать прямій у=5

г) складіть рівняння кола з діаметром АС

РІШЕННЯ:

а) так як точка М – є серединою відрізку, знайдемо її координати за формулою середини відрізка:

$\\ \\ Xm= \frac{Xa+Xb}{2} = \frac{ - 2 + 0}{2} = \\ \\ = \frac{ - 2}{2} = - 1 \\ \\ Ym = \frac{Ya+Yb}{2} = \frac{ - 1 + 5}{2} = \frac{4}{2} = \\ = 2$

M(–1; 2)

ВІДПОВІДЬ: M(–1; 2)

б) Для того щоб знайти довжину відрізка NN треба знайти координати точки N, яка належить відрізку ВС за попередньою формулою середини відрізка:

$\\ \\ Xn = \frac{Xb + Xc}{2} = \frac{0 + 6}{2} = \frac{6}{2} = 3 \\ \\ Yn = \frac{Yb+Yc}{2} = \frac{5 + 5}{2} = \frac{10}{2} = \\ \\ = 5$

N(3; 5)

найдемо довжину відрізка MN за формулою:

MN²=(Хn–Xm)²+(Yn–Ym)²=(3–(–1))²+(5–2)²=

=(3+1)²+3²=4²+9=16+9=25

MN=√25=5

ВІДПОВІДЬ: MN=5

в) пряма у=5 паралельна осі ОХ і при цьому Х=0, тому прямій у=5 належать точки, у яких координата у дорівнює 5 – це точки В, N і С

ВІДПОВІДЬ: В, N і С

г) Знайдемо координати середини відрізка АС, щоб визначити центр кола, нехай центром кола буде точка О:

$Xo=\displaystyle \displaystyle \frac{-2+6}{2} =\frac{4}{2} =2 \\ \\ \displaystyle \displaystyle Yo=\frac{-1+5}{2} =\frac{4}{2} =2$

О(2; 2) – координати центра кола;

Початкове рівняння кола:

(х–а)²+(у–b²)=R², де а та b – координати кола, а R – його радіус. Координати центру відомі, і так як радіус дорівнює половині діаметра АС, і середня лінія також дорівнює половині АС, то R=5.

Підставимо дані у формулу:

(х–а)²+(у–b²)=R²

(х–2)²+(у–2)²=5²

(х–2)²+(у–2)²=25 – шукане рівняння