Question

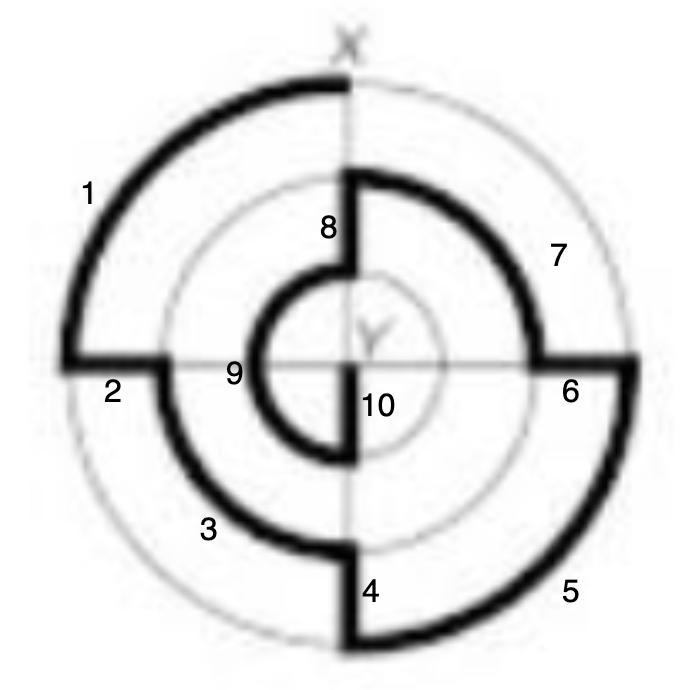
№2. На рисунке 2 даны три круга радиусов 100 см, 200 см и 300 см, имеющие общий центр. Мышка пробежала из края большого круга (точки Х) до центра (до точки Y) по выделенной жирной траектории. Сколько сантиметров пробежала мышка? Считайте, что п = 3,14.​

Answer 1

Ответ:

Мышка пробежала 2384 см.

Пошаговое объяснение:

На рисунке 2 даны три круга радиусов 100 см, 200 см и 300 см, имеющие общий центр. Мышка пробежала из края большого круга (точки Х) до центра (до точки Y) по выделенной жирной траектории. Сколько сантиметров пробежала мышка? Считайте, что π = 3,14.​

Даны радиусы окружностей:

R₁ = 100 см, R₂ = 200 см; R₃ = 300 см.

Рассмотрим путь мышки.

Он состоит из 10 участков.

2; 4; 6; 8 и 10 - прямолинейные, 1; 3; 5; 7; 9 - мышка двигалась по дугам окружностей.

Найдем длины этих участков:

уч.2 = уч.4 = уч.6 = R₃ - R₂ = 300 - 200 = 100 (см)

уч.8 = R₂ - R₁ = 200 - 100 = 100 (см)

уч.10 = R₁ = 100 см.

Найдем сумму длин прямолинейных участков:

100 · 3 + 100 + 100 = 500 (см)

Теперь разберемся с длинами дуг.

• Длина дуги равна:

        С = 2πR

Дуги 1 и 5 равны четверти окружности с радиусом R₃:

$\displaystyle C_1=C_5=\frac{2\pi R_3}{4}=\frac{\pi \cdot 300}{2} =150\pi$  (см)

Дуги 3 и 7 равны четверти окружности с радиусом R₂:

$\displaystyle C_3=C_7=\frac{2\pi R_2}{4}=\frac{\pi \cdot 200}{2} =100\pi$  (см)

Дуга 9 равна половине окружности с радиусом R₁:

$\displaystyle C_9=\frac{2\pi R_1}{2}=100\pi$  (см)

Найдем длины всех дуг:

150π · 2 + 100π · 2 + 100π = 600π = 1884 (см)

Сложим длины прямолинейных участков и дуг:

1884 + 500 = 2384 (см)

Мышка пробежала 2384 см.

#SPJ1