Предмет: Алгебра,
автор: Gama563
1. Разложите на множители: а) 2,25a²-0,4962; в) -1,44x y8+25; д) 9х2+у2+6ху-6cx-2cy; ж) 2 ; a12+b9; 10 27 7 6) 1 m2-1 9 г) е) - 3) 13 36 36(u+1)2-25(2u-1)2; 15 nt; +1; m2+5m+5n-n². 8 ПОМОГИТЕ ПЖ СРОЧНО НАДО
Приложения:
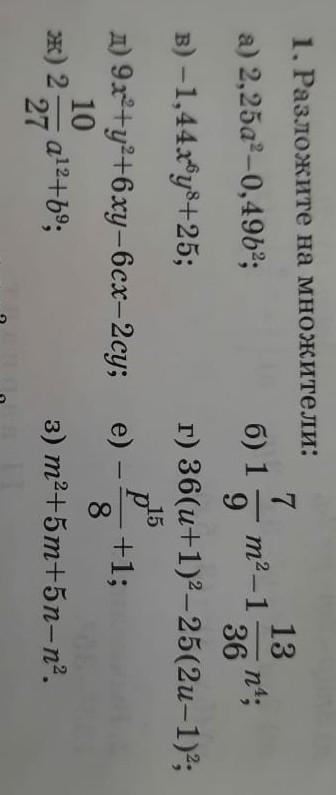
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1. a)
б)
в)
г)
д)
е)
ж)
з)
masha01021:
здравствуйте, помогите пожалуйста
Похожие вопросы
Предмет: Українська література,
автор: dghd9047
Предмет: Английский язык,
автор: zhenyaantipova103
Предмет: Қазақ тiлi,
автор: hati401
Предмет: Русский язык,
автор: SonicDeinv
Предмет: Английский язык,
автор: gordienkolada851