Предмет: Алгебра,
автор: Аноним
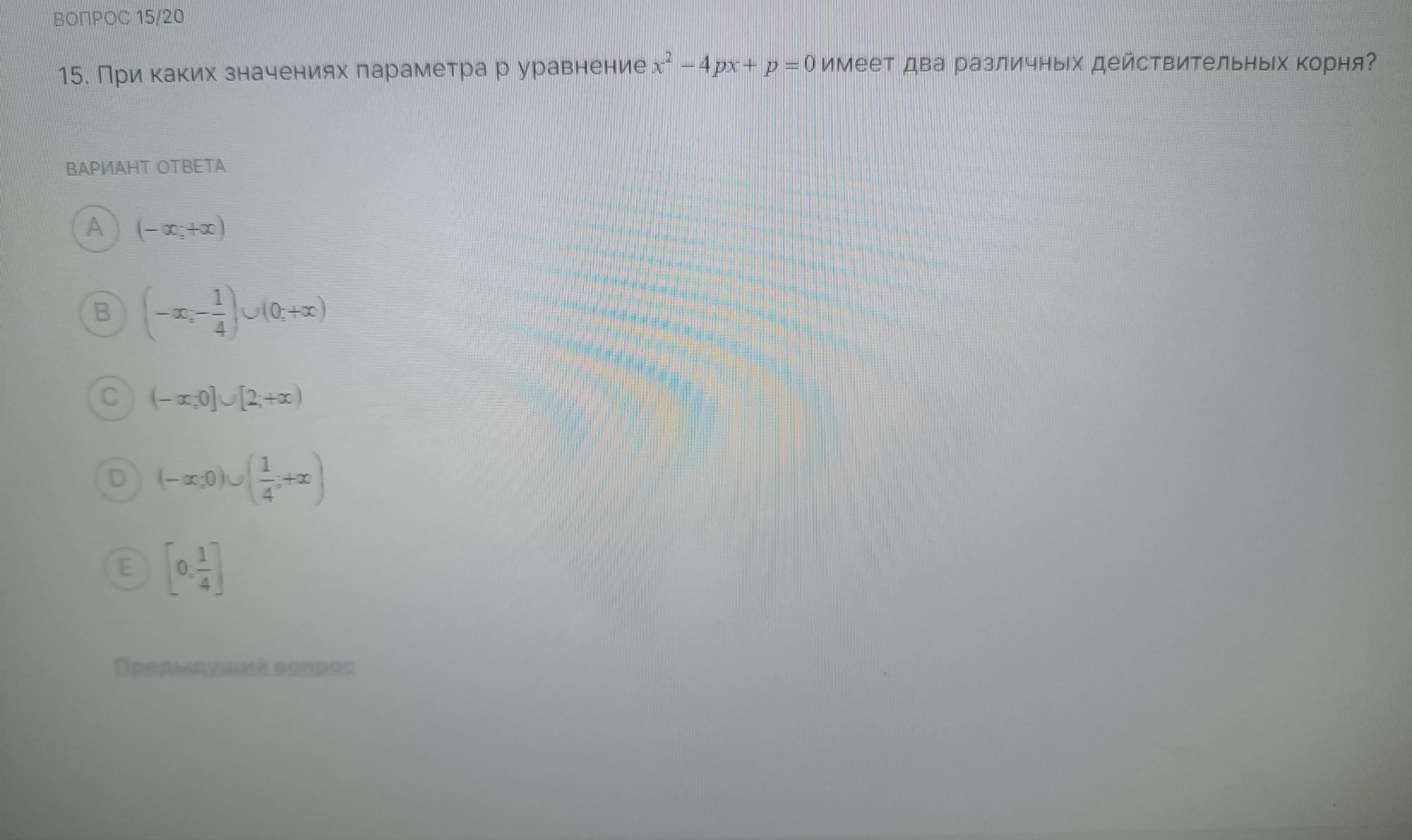
15. При каких значениях параметра р уравнениеx²-4px+p=0 имеет два различных действительных корня? ВАРИАНТ ОТВЕТА A (-00;+00) (-∞;-1)+0+ C (-∞0:0] [2:+00) Ⓒ-mol (1+0) B E 11 I (0;+00)
Приложения:
Ответы
Автор ответа:
1
Відповідь:
Для того, чтобы квадратное уравнение x² - 4px + p = 0 имело два различных действительных корня, необходимо и достаточно, чтобы дискриминант был положительным: D = b² - 4ac > 0, где a = 1, b = -4p, c = p.
Подставляя значения коэффициентов, получаем:
(-4р)² - 4·1·р > 0
16р² - 4р > 0
4р(4р - 1) > 0
Таким образом, два различных действительных корня будут у уравнения x² - 4px + p = 0 при значениях параметра p из интервала (-∞; 0) ∪ (1/4; +∞). Ответ: вариант ответа C.
Пояснення:
Похожие вопросы
Предмет: Алгебра,
автор: karin4ik638
Предмет: Математика,
автор: lorilorieva
Предмет: История,
автор: mirgaliyeva82
Предмет: Обществознание,
автор: nidzatgusejnov7
Предмет: Литература,
автор: 11Колбаса11