Предмет: Алгебра,
автор: ezzamarria
Решите неравенство:.
Приложения:
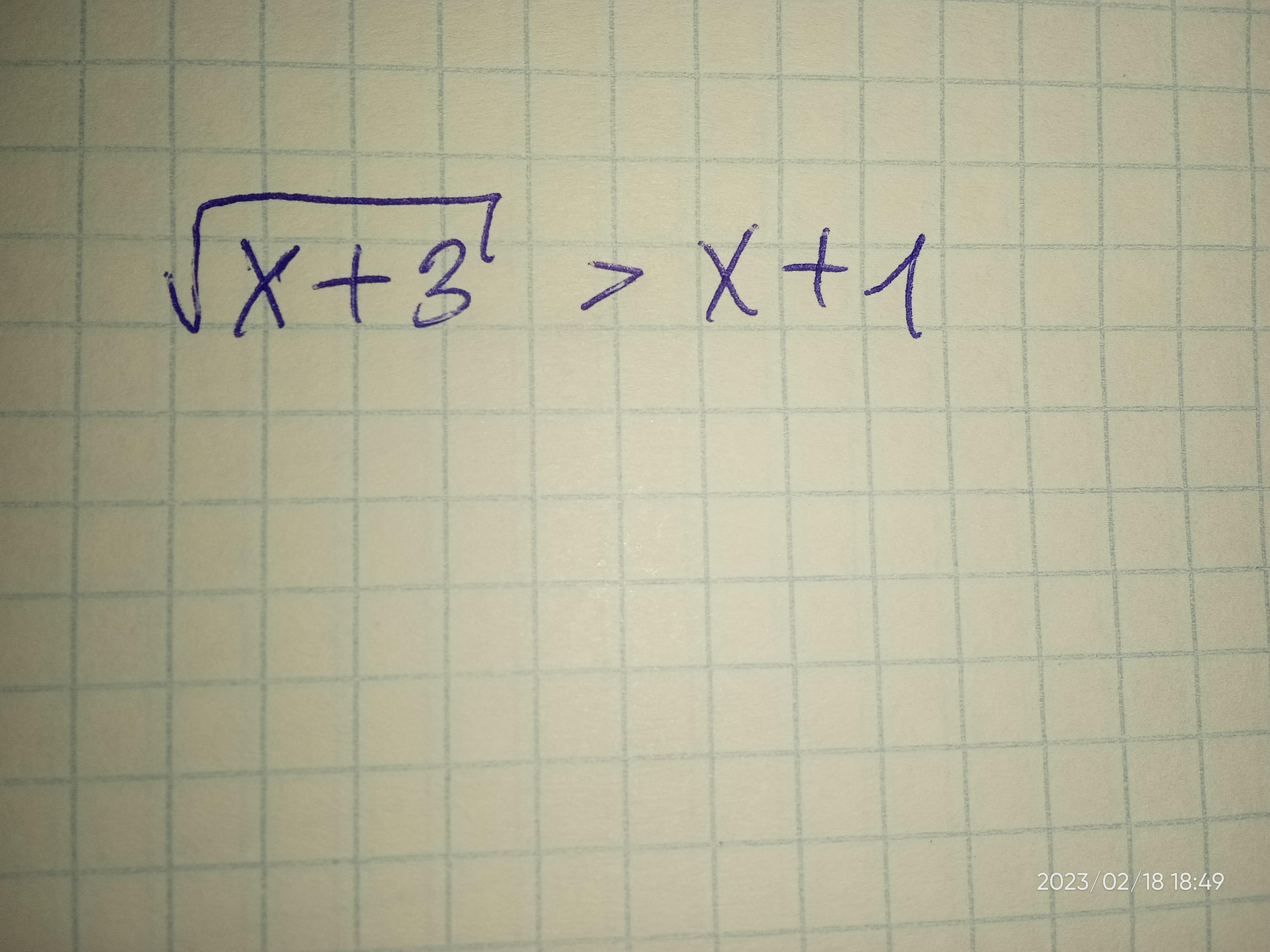
Ответы
Автор ответа:
0
Ответ:
x ∈ [ - 3 ; 1 )
Объяснение:
Вспомним , что неравенство
равносильно совокупности двух систем :
Соответственно :
Похожие вопросы
Предмет: Математика,
автор: boskunchievb
Предмет: Українська мова,
автор: evelina33398
Предмет: Информатика,
автор: pykikaki
Предмет: Алгебра,
автор: uliana112
Предмет: Алгебра,
автор: 111111DA