ПОМОГИТЕ СРОЧНО РЕШИТЬ!ДАЮ 100 БАЛОВ
Помогите решить неравенство
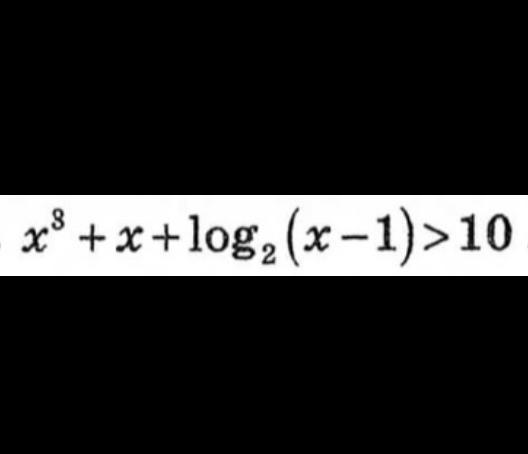
Ответы
x > 1
f(x) = x⁸ + x + log²(x - 1) - 10.
Вычислим производную функции f(x):
f'(x) = 8x⁷ + 1 + 2log(x - 1)/(x - 1)
8x⁷ + 1 + 2log(x - 1)/(x - 1) = 0
2log(x - 1)/(x - 1) = -1 - 8x⁷
log(x - 1) = (1 + 8x⁷)/(1 - x)
x - 1 = 10^( (1 + 8x⁷)/(1 - x) )
Полученное уравнение решить аналитически не удается, поэтому воспользуемся численными методами для нахождения корней. Заметим, что x > 1, поэтому можно использовать метод половинного деления, начиная поиск с интервала [1, 2]:
при x ≈ 1, f(x) < 0
при x ≈ 1,28, f(x) > 0
при x ≈ 1,29, f(x) < 0
Таким образом, на интервале [1, 1.28] функция f(x) отрицательна, на интервале [1.28, 1.29] - положительна, на интервале [1.29, ∞) - отрицательна.
решением исходного неравенства является множество всех x > 1, кроме интервала [1.28, 1.29]:
x ∈ (1, 1.28) ∪ (1.29, +∞)