срочна..................

Ответы
Ответ: 1 Д; 2Б; 3А; 4В
Решение:
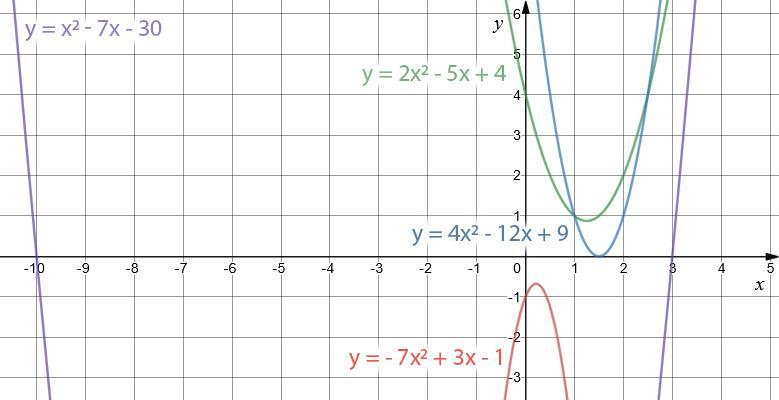
наиболее быстрым способом решения будет графический (см. рисунок)
решением х² + 7х - 30 ≥ 0 является (-∞; -10]∪[3; ∞); 1 Д
решением 2х² -5х +4 ≤ 0 является ∅ (нет решений) 2 Б
решением 4х² -12х +9 ≤ 0 является одна точка на графике, когда у = 0, т.е. {1,5}; 3А
решением -7х² + 3х - 1 < 0 является (-∞; ∞); 4 B
Відповідь: 1-Д, 2-Б, 3-А, 4-В.
Пояснення:
Спочатку треба визначити дискримінант кожного із квадратного тричлена. Визначити з чотирьох нерівностей ті, у яких D<0 , вони мають пусту множину або нескінченності (всі дійсні числа) .
1. D>0, 2. D<0, 3. D=0, 4. D<0.
Починаємо з аналізу 2 та 4.
2. а>0, вітки угору, не перетинає вісь 0х, не набуває від'ємних та нуль значень, тому Б.
4. а< 0, вітки униз, не перетинає вісь 0х, набуває тільки від'ємних значень на області визначення. Тому В.
Далі 3, де D=0. Одна точка дотику, вітки вгору, тому А.
Залишається 1 нерівність. Має точки перетину з 0х, за теоремою Вієта вони очевидні, тому Д.