Question

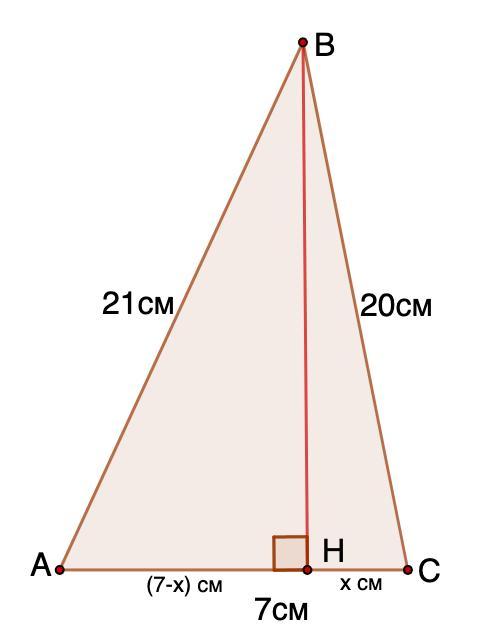
Знайдіть більшу висоту трикутника, сторони якого дорівнюють 20 см, 21 см і 7 см.​

Answer 1

Ответ:

Большая высота треугольника равна (24√34)/7 см.

Пошаговое объяснение:

Найдите большую высоту треугольника, стороны которого равны 20 см, 21 см и 7 см.​

Дано: ΔАВС.

АВ = 21 см; ВС = 20 см; АС = 7 см.

Найти: большую высоту.

Решение:

• Большая высота треугольника проведена к меньшей стороне.

Меньшая сторона АС.

Проведем высоту ВН.

Рассмотрим ΔАВН и ΔНВС - прямоугольные.

Пусть НС = х см; Тогда АН = (7 - х) см.

По теореме Пифагора:

Из ΔАВН:

ВН² = АВ² - АН²  

⇒   ВН² = 441 - (7-х)² = 441 - 49 + 14х - х² = -х² + 14х + 392   (1)

Из ΔНВС:

ВН² = ВС² - НС²

⇒ ВН² = 400 - х²     (2)

Приравняем (1) и (2):

-х² + 14х + 392 = 400 - х²

14х = 8

х = 8/14

х = 4/7

ВН² = 400 - (4/7)² =

$\displaystyle =\frac{19600-16}{49} =\frac{19584}{49}$

$\displaystyle BH=\frac{24\sqrt{34} }{7}$  (см)

Большая высота треугольника равна (24√34)/7 см.

Можно решить эту задачу при помощи формулы Герона.

Площадь треугольника равна:

$\displaystyle \bf S=\sqrt{p(p-a)(p-b)(p-c)}$,

где р - полупериметр, a, b, c - стороны треугольника.

р = (21 + 20 + 7) : 2 = 24 (см)

$\displaystyle \bf S=\sqrt{24(24-21)(24-20)(24-7)}=\sqrt{24\cdot3\cdot4\cdot17}=12\sqrt{34}$   (см)

С другой стороны площадь треугольника равна:

                S = 1/2 ah,

где а - сторона треугольника, h - высота, проведенная к этой стороне.

$\displaystyle S=\frac{1}{2}AC\cdot BH\\ \\12\sqrt{34}=\frac{1}{2} \cdot7\cdot BH\\\\BH=\frac{24\sqrt{34} }{7}$(см)

#SPJ1