СПАСАЙТЕ СРОЧНО!!!
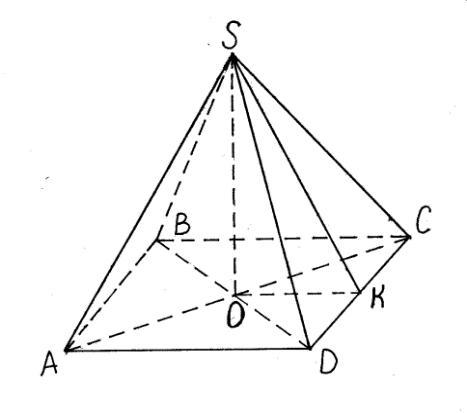
Відстань від точки S до площини квадрата АВСD
дорівнює 3√5 см. Периметр квадрата дорівнює 48 см.
Користуючись рисунком, виберіть правильну умову:
А) SB < SK ; Б) OD = 6 см; В) OC > OD;
Г) SK = 9 см.
Ответы
Ответ:
Г) SK=9см
Объяснение:
А)
SK- перпендикуляр до сторони DC.
∆SDK- прямокутний трикутник.
SD- гіпотенуза.
SD=SB=SC=SA.
SD>SK, гіпотенуза більше катета.
SB>SK
___________
Б)
Р=4*АВ;
АВ=Р/4=48/4=12см
BD=AB√2=12√2см діагональ квадрата
ВO=OD, властивості квадрата.
ОD=BD/2=12√2/2=6√2см
OD=6√2см
____________
В)
Діагоналі квадрата рівні, властивості квадрата
BD=AC.
Діагоналі квадрата точкою перетину поділяються навпіл, властивості квадрата.
ОC=OD=AO=BO
OC=OD
_____________
Г)
SO=3√5см
ОК=АВ/2=12/2=6см
∆SOK- прямокутний трикутник.
За теоремою Піфагора:
SK=√(SO²+OK²)=√(6²+(3√5)²)=
=√(36+45)=√81=9см
Розв'язання:
SO = 3√5 см; Pabcd = 42 см.
Pabcd = 4·AB
48 = 4·AB
AB = 12(см)
1) Знайдемо діагональ квадрата ABCD:
AC = BD = √2·AB
AC = BD = √2·12 = 12√2(см)
Діагоналі квадрата точкою перетину діляться навпіл, тому AO = OC = OB = OD = 12√2/2 = 6√2(см)
Отже, твердження Б) ми виключаємо, як неправильне.
Твердження В) також, оскільки діагоналі діляться точкою перетину навпіл і вони рівні, звідси OC = OD.
2) З ∆SOB(∠SOB = 90°; OB = 6√2 см; SO = 3√5 см)
За темою Піфагора:
SB² = OB²+SO²
SB = √(OB²+SO²)
SB = √((6√2)² + (3√5)²) = √(72+45) = 3√13 (см)
3) OK – це половина середньої лінії квадрата ABCD, оскільки середня лінія квадрата дорівнює його стороні, то її половина: OK = 1/2·AB;
OK = 1/2·12 = 6(см)
Тепер, перейдемо до ∆SOK( ∠SOK = 90°; OK = 6 см; SO = 3√5 см)
За теоремою Піфагора:
SK² = OK²+SO²
SK = √(OK²+SO²)
SK = √(6²+(3√5)²) = √(36+45) = √81 = 9 (см)
SK = 3√13 ≈ 10.8 см, тому SB > SK, тобто твердження
А) також неправильне.
Отже, залишається Г), до того ж ми вже визначили, що він правильний.
Відповідь: Г) SK = 9 см.