Question

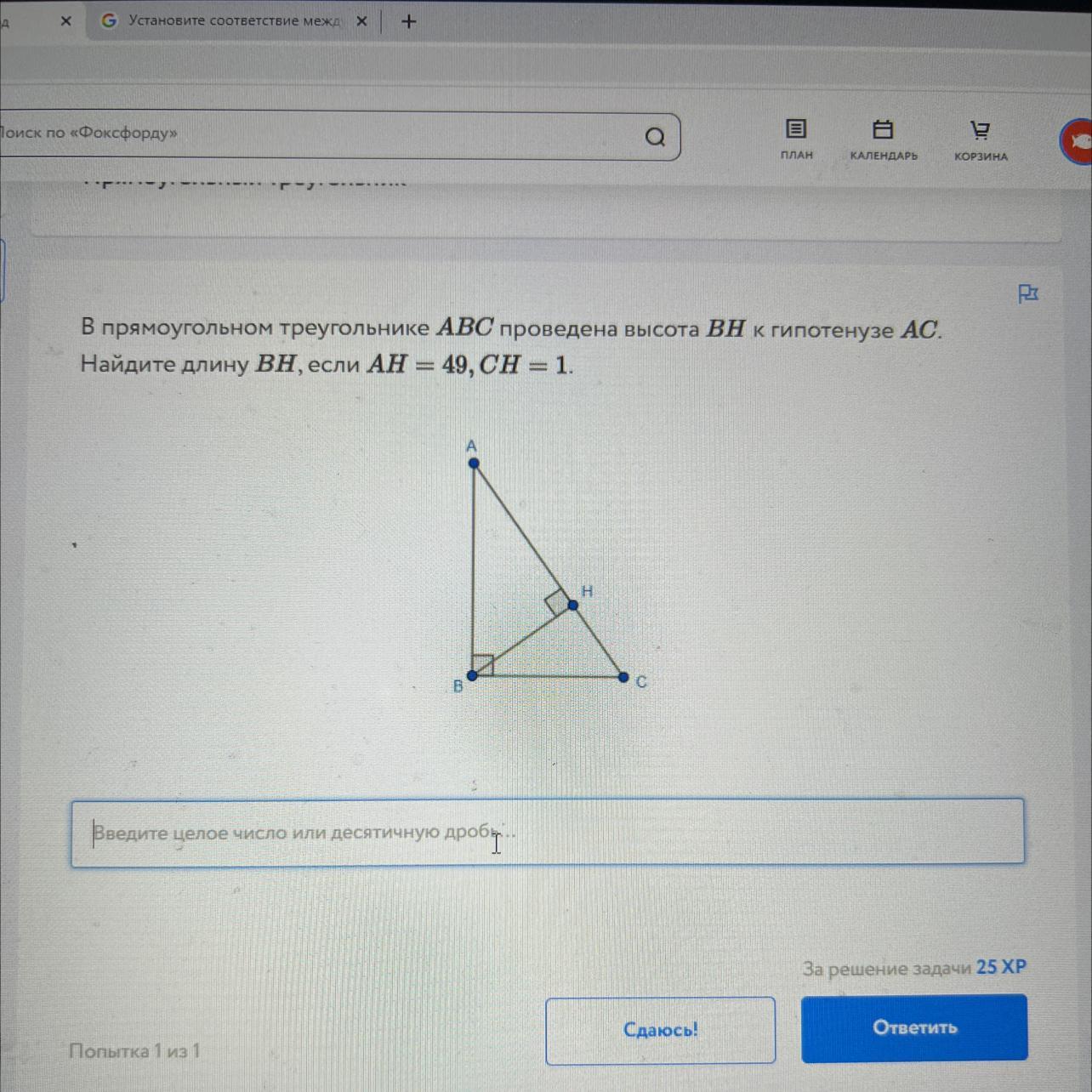
В прямоугольном треугольнике ABC проведена высота ВН к гипотенузе AC.
Найдите длину ВН, если АН = 49, СН = 1.

Answer 1

Ответ:

У нас есть прямоугольный треугольник ABC с гипотенузой AC, высотой ВН и катетами AB и BC. Знаем, что АН = 49 и СН = 1.

Так як ВН - высота, то у нас есть два подобных прямоугольных треугольника ABN и BCN:

ABN:

AB^2 = AN * BN, тому BN = AB^2 / AN

BCN:

BC^2 = CN * BN, тому BN = BC^2 / CN

Отже,

AB^2 / AN = BC^2 / CN

Замінюємо AN і CN:

AB^2 / 49 = BC^2

Таким чином, ми можемо виразити довжину катета AB через довжину гипотенузи AC:

AB = sqrt(49 * BC^2) = 7BC

Також ми знаємо, що:

BN = AB^2 / AN = (7BC)^2 / 49 = BC^2 / 7

Застосовуючи теорему Піфагора до прямокутного трикутника BCN, ми можемо знайти довжину ВН:

BN^2 + CN^2 = BC^2

(BC^2 / 7)^2 + 1^2 = BC^2

BC^4 / 49 + 1 = BC^2

BC^4 + 49 = 49BC^2

BC^4 - 49BC^2 + 49 = 0

Застосовуючи формулу квадратного кореня, отримуємо:

BC^2 = (49 ± sqrt(49^2 - 4149)) / 2

BC^2 = (49 ± 7sqrt(3)) / 2

Оскільки BC має бути менше AC, то ми беремо значення BC, яке є коренем меншим за AC:

BC^2 = (49 - 7sqrt(3)) / 2

BC = sqrt((49 - 7sqrt(3)) / 2)

Тоді довжина ВН дорівнює:

BN = BC^2 / 7 = (49 - 7sqrt(3)) / 14