Предмет: Математика,
автор: cosmi2936
ХЭЛП ДАЮ 40 БАЛЛОВ! СРОЧНО!!
Приложения:
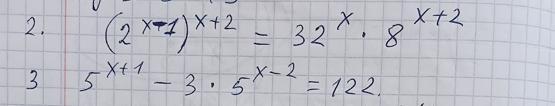
Ответы
Автор ответа:
0
Ответ:
Применяем свойства степеней : .
Приведём левую и правую части равенства к одному основанию.
Похожие вопросы
Предмет: Математика,
автор: yevasto
Предмет: Українська мова,
автор: Аноним
Предмет: Алгебра,
автор: 95twv8mz4y
Предмет: Українська мова,
автор: Аноним