Предмет: Геометрия,
автор: sashaostrovska008
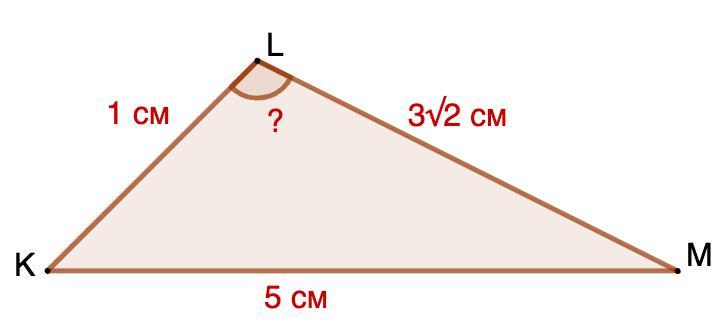
У трикутнику KLM КМ = 5 см, KL = 1 см, LM = 3√2 см. Знайдіть градусну міру найбільшого кута трикутника.
Ответы
Автор ответа:
4
Ответ:
Градусная мера наибольшего угла треугольника равна 135°.
Объяснение:
В треугольнике KLM КМ = 5 см, KL = 1 см, LM = 3√2 см. Найдите градусную меру наибольшего угла треугольника.
Дано: ΔKLM;
КМ = 5 см, KL = 1 см, LM = 3√2 см.
Найти: градусную меру наибольшего угла треугольника.
Решение:
КМ = 5 см, KL = 1 см, LM = 3√2 см ≈ 4,2 см.
- Против большей стороны в треугольнике лежит больший угол.
Большая сторона КМ = 5 см ⇒ больший угол L.
- Воспользуемся теоремой косинусов:
- Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
⇒ ∠L = 135°
Градусная мера наибольшего угла треугольника равна 135°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Химия,
автор: kuratnyknikita
Предмет: Химия,
автор: vikysishevchenkoo
Предмет: Математика,
автор: tgrisina59
Предмет: Математика,
автор: BROTANHIK
Предмет: Математика,
автор: Kustovsavelij2