Question

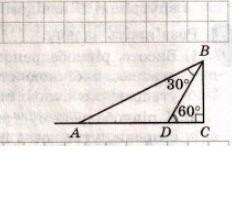
5 Розв'яжіть задачу за рисунком. 1) Знайдіть АC, якщо AD=12 см. 2) Знайдіть АC, якщо DC=5 см.
ДАЮ 100 БАЛОВ
​

Answer 1

Ответ:

1) AС = 18 см

2) АС = 15 см

Объяснение:

• Катет прямокутного трикутника, що лежить проти кута 30°,дорівнює половині гіпотенузи (гіпотенуза удвічі довша від катета навпроти кута 30°.)
• Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.

1.

Дано: △АВС(∠С=90°), ∠ABD=30°, ∠BDC=60°, AD=12см

Знайти: АС

1) Так як ∠BDC - зовнішній кут △АВD, то ∠А+∠ABD=∠BDC, ⇒

∠A=∠BDC-∠ABD=60°-30°=30°

∠A=∠ABD=30° ⇒ △ABD - рівнобедрений з основою АВ.

BD=AD=12 (см)

2) Розглянемо прямокутний трикутник BDC(∠C=90°)

За теоремою про суму кутів прямокутного трикутника знайдемо кут DBC:

∠DBC=90°-∠BDC=90-60°= 30°

3) Катет DC лежить проти кута 30°. Тому:

DC= ½•BD=½•12= 6 (см)

4) АС = AD+DC = 12+6 = 18 (см)

Відповідь: 18 см

2.

Дано: △АВС(∠С=90°), ∠ABD=30°, ∠BDC=60°, DС=5 см

Знайти: АС

1) Розглянемо прямокутний трикутник BDC(∠C=90°)

За теоремою про суму кутів прямокутного трикутника знайдемо кут DBC:

∠DBC=90°-∠BDC=90-60°= 30°

2) Катет DC лежить проти кута 30°. Тому гіпотенуза BD удвічі його більша:

BD=2•DC=2•5= 10 (см)

3)Так як ∠BDC - зовнішній кут △АВD, то ∠А+∠ABD=∠BDC, ⇒

∠A=∠BDC-∠ABD=60°-30°= 30°

∠A=∠ABD=30° ⇒ △ABD - рівнобедрений з основою АВ.

AD=BD=10 (см)

4) AC=AD+DC=10+5= 15 (см)

Відповідь: 15 (см).

#SPJ1