Предмет: Геометрия,
автор: kirskeleton016
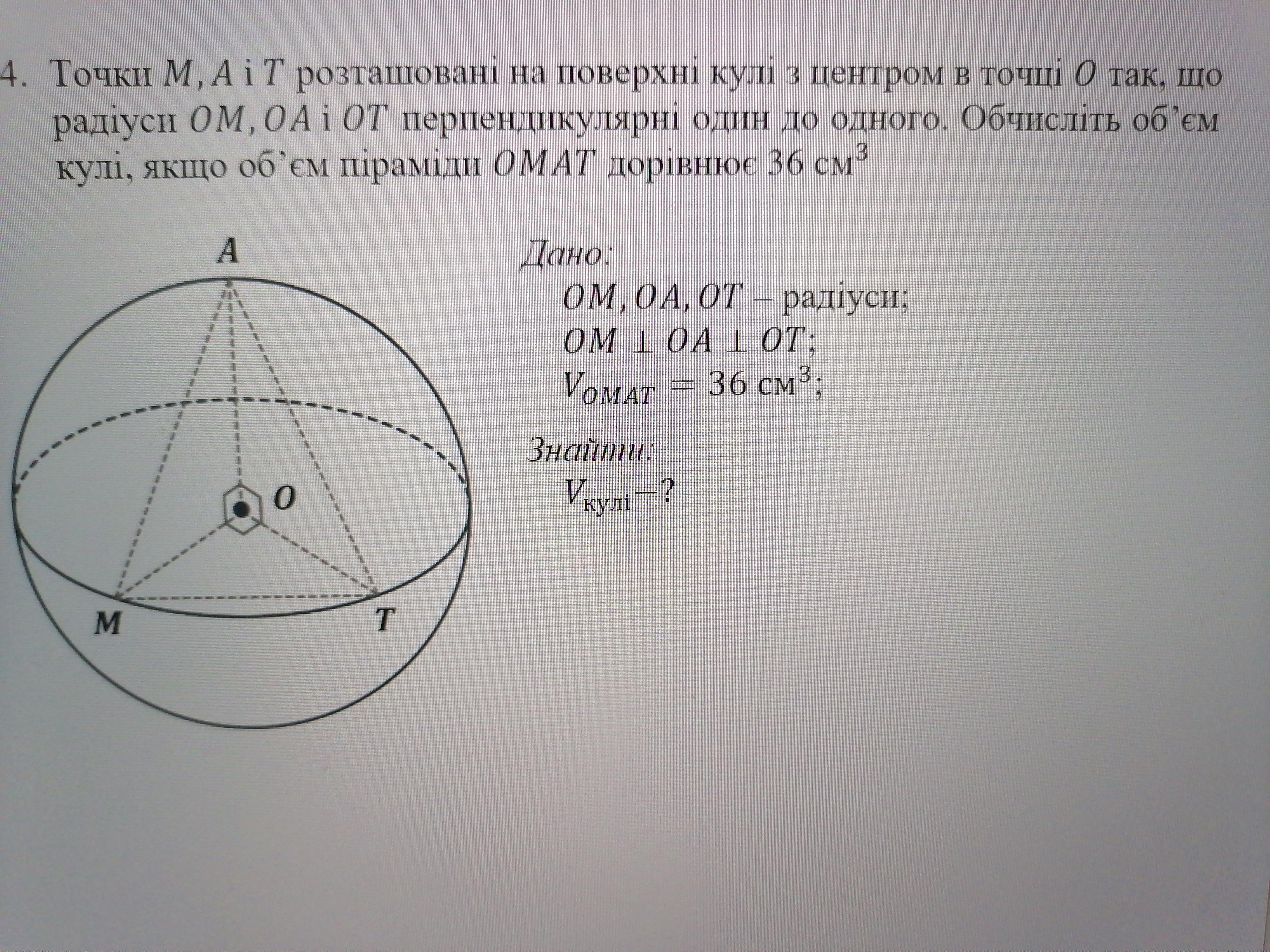
Точки М, А і Т зозташовані на поверхні кулі з центром в точці О так, що радіуси ОМ, ОА і ОТ перпендикулярні один до одного. Обчисліть об'єм кулі, якщо об'єм піраміди ОМАТ дорівнює 36 см³
Приложения:
Ответы
Автор ответа:
2
Ответ:
Объем шара равен 288π см³.
Объяснение:
4. Точки M, A и T, расположенные на поверхности шара с центром в точке о так, что радиусы OM, OA и ОТ перпендикулярны друг к другу. Вычислите объем шара, если объем пирамиды равен 36 см³.
Дано: Шар(О, R);
ОМ, ОА, ОТ - радиусы;
ОМ ⊥ ОА ⊥ ОТ;
V (ОМАТ) = 36 м³.
Найти: Vшара.
Решение:
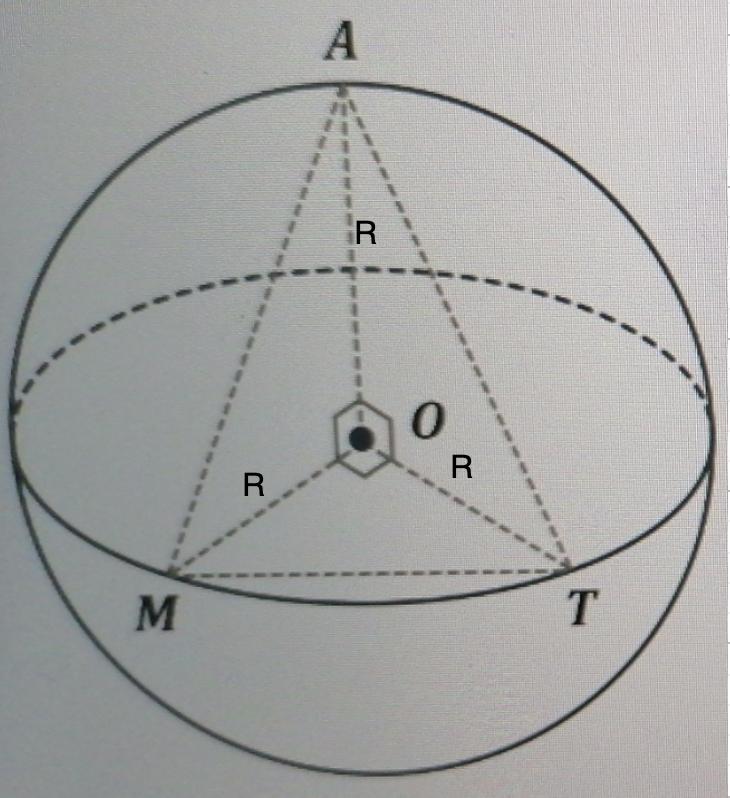
Рассмотрим ОМАТ.
- Объем пирамиды вычисляется по формуле:
, где h - высота.
Основание пирамиды - ΔМОТ - прямоугольный.
МО = ОТ = R
- Площадь прямоугольного треугольника равна половине произведения катетов.
, где a и b - катеты.
⇒
OA = R - высота пирамиды.
Тогда объем пирамиды равен:
- Объем шара вычислим по формуле:
⇒
Объем шара равен 288π см³.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Физика,
автор: gamego77
Предмет: Українська мова,
автор: kuzmicdarina54
Предмет: Математика,
автор: i31154267
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: bogdansvica