Предмет: Алгебра,
автор: Callisstto
a) Запишите уравнение вертикальной асимптоты.
b) Составьте уравнение наклонной асимптоты.
Приложения:
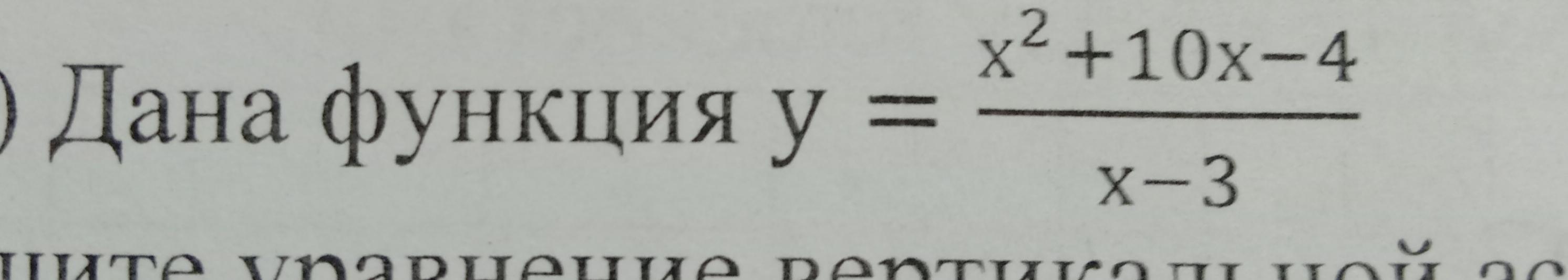
Ответы
Автор ответа:
1
Ответ:
а) х = 3
b) y = x + 13
Объяснение:
Дана функция у = (х²+10х-4)/(х-3)
а) Знаменатель не должен быть равен нулю:
х - 3 ≠ 0
х ≠ 3
То есть область определения D(y) = (-∞;3)U(3;+∞).
- Прямая х=а называется вертикальной асимптотой к графику функции y=f(x), если хотя бы один из односторонних пределов , равен +∞ или -∞.
Находим эти пределы:
Таким образом x = 3 - уравнение вертикальной асимптоты.
b) Наклонная асимптота имеет вид у = кх + b
Она существует при условии существования пределов:
Найдём к:
Найдем b:
Следовательно , у = х + 13 - уравнение наклонной асимптоты.
Похожие вопросы
Предмет: Английский язык,
автор: ewalutsk
Предмет: Математика,
автор: erachin77
Предмет: Другие предметы,
автор: polinkahailova
Предмет: Математика,
автор: daracerencova
Предмет: Математика,
автор: 20003266