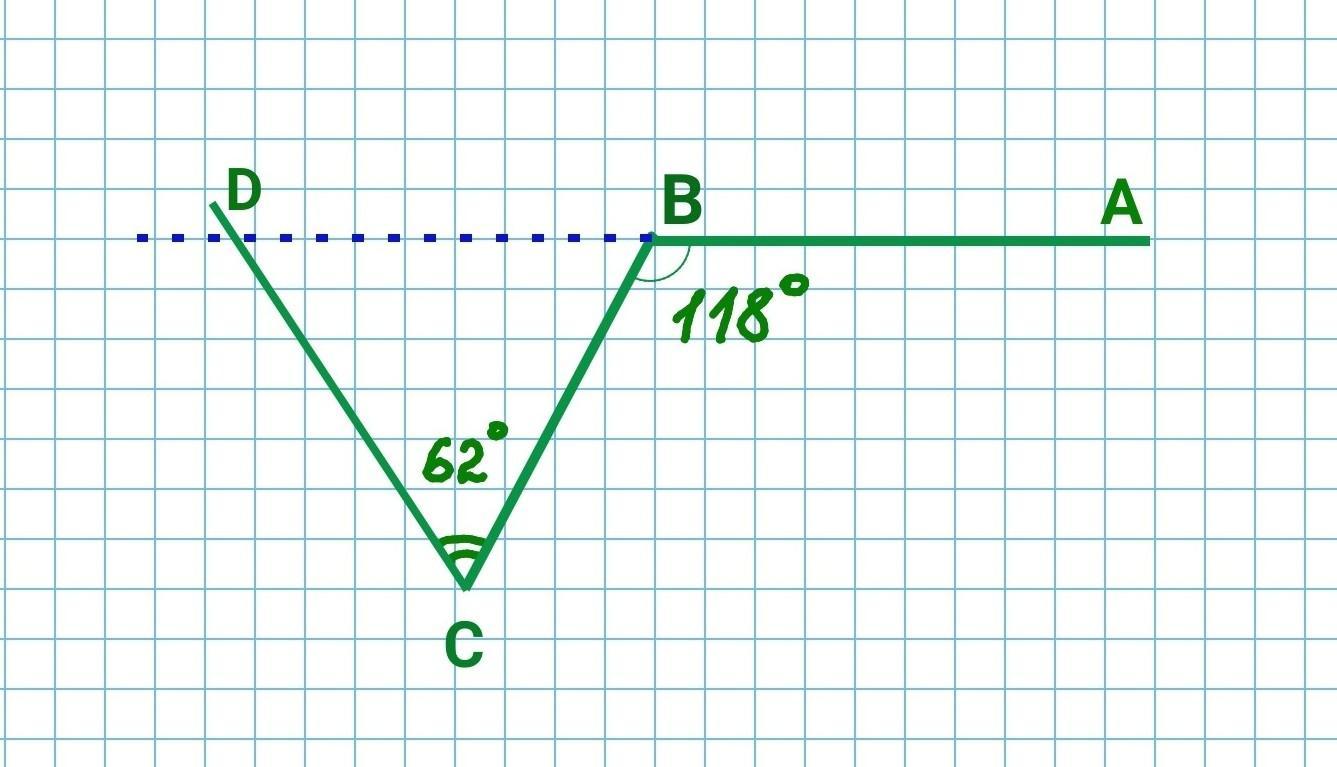
19. Угол АВС равен 118°. Угол BCD равен 62°. Могут ли быть прямые АВ и CD: а) параллельными; b) пересекающимися?
Дам 40 баллов
Ответы
Ответ:
Прямые AB и CD могут быть параллельными, если точки А и D лежат по одну сторону от прямой ВС, и пересекающимися, если точки А и D лежат по по разные стороны от прямой ВС.
Объяснение:
Угол АВС равен 118°. Угол BCD равен 62°. Могут ли быть прямые АВ и CD: а) параллельными; b) пересекающимися?
Признаки параллельности прямых:
- Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
- Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Дано: ∠ABC=118°, ∠BCD=62°.
Могут ли прямые AB и CD быть: а) параллельными; b) пересекающимися?
Решение
а) если точки А и D лежат по одну сторону от прямой ВС, то ∠ABC и ∠BCD - внутренние односторонние углы при прямых AB и CD и секущей ВС.
∠ABC +∠BCD = 118°+62°=180°
По признаку параллельности прямых AB || CD.
б) если точки А и D лежат по разные стороны от прямой ВС, то ∠ABC и ∠BCD - внутренние накрест лежащие углы при прямых AB и CD и секущей ВС.
∠ABC ≠∠BCD, так как 118°≠62°.
⇒ АВ∦CD, а значит AB и CD пересекаются.
Ответ: а) да; б) да
#SPJ1