Предмет: Алгебра,
автор: manzheleyartem
Алгебра-8клас даю 100 балов
Приложения:
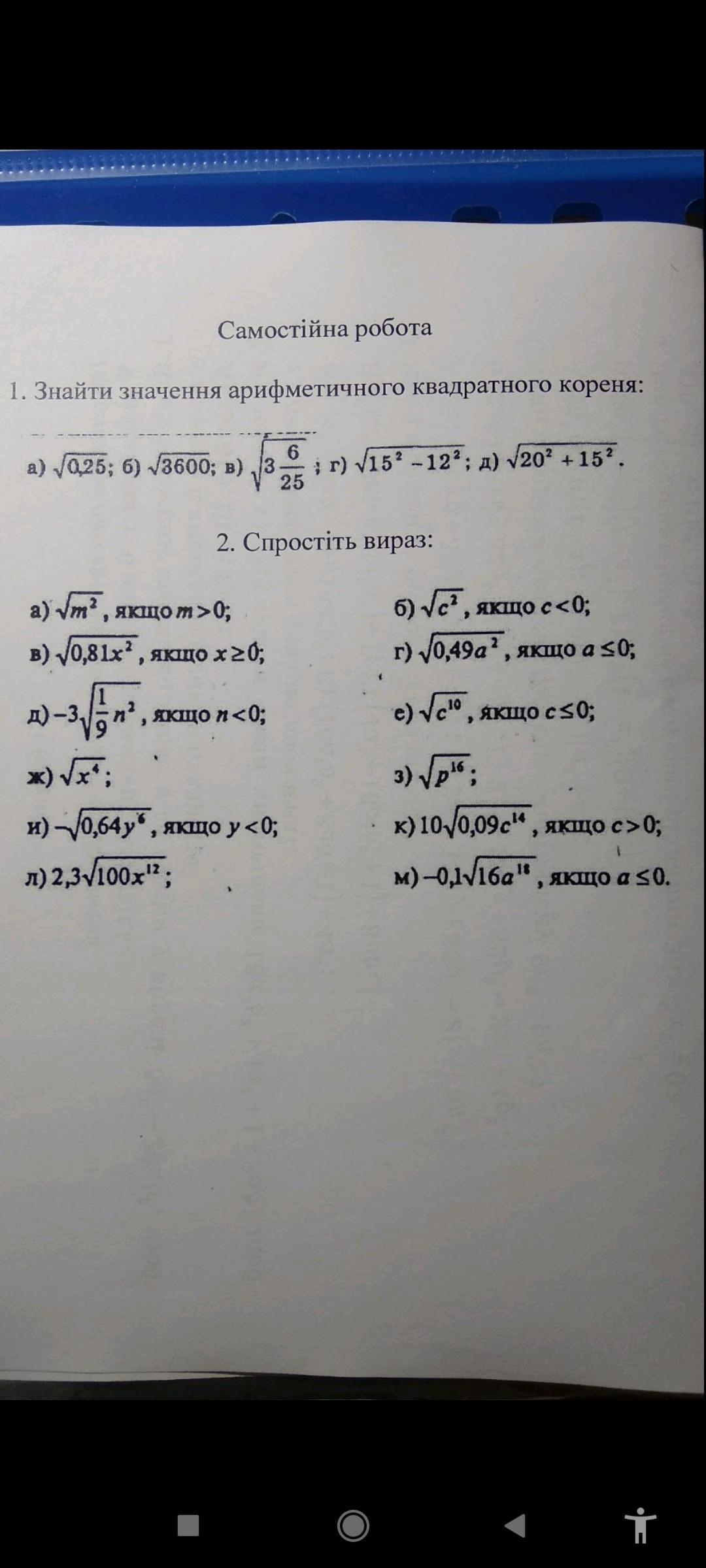
Ответы
Автор ответа:
1
Ответ:
Арифметический квадратный корень может принимать только
неотрицательные значения, то есть . И подкоренное
выражение должно быть неотрицательным , .
2) Упростить выражение . Применяем правило извлечения квадратного корня из выражения, содержащего переменную . Важно учитывать знак переменной .
Похожие вопросы
Предмет: Английский язык,
автор: likeyal
Предмет: Химия,
автор: denisseychuk
Предмет: Химия,
автор: aftonballora17
Предмет: Математика,
автор: damirsafarov86105
Предмет: Английский язык,
автор: minakimth777