Предмет: Математика,
автор: Hamidjajajaj
По рисунку найдите площадь правильного многоугольника.Точка О центр многоугольника
Приложения:

Ответы
Автор ответа:
3
Ответ:
a) 256 (ед. кв.)
b) (ед. кв.)
c) (ед. кв.)
Пошаговое объяснение:
Нужно знать:
1) В любой правильный многоугольник можно вписать окружность, и притом только одну.
2) Площадь S₄ правильного четырёхугольника, то есть квадрата, через радиус r вписанной окружности выражается формулой:
3) Площадь S₃ правильного треугольника, то есть равностороннего треугольника, через радиус r вписанной окружности выражается формулой:
4) Площадь S₆ правильного шестиугольника через радиус r вписанной окружности выражается формулой:
Решение. В каждый из многоугольников впишем окружность (см. рисунок). Тогда перпендикуляры к сторонам многоугольника будут радиусами вписанных окружностей. Вычислим площади:
a) r = 8, то
b) r = 6, то
c) r = 12, то
#SPJ1
Приложения:
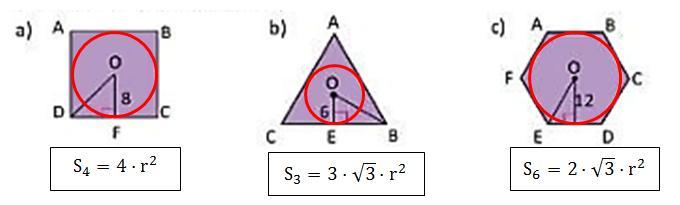
Похожие вопросы
Предмет: География,
автор: Angelina9525
Предмет: Информатика,
автор: kawyn2209
Предмет: Математика,
автор: 123brawlstars37
Предмет: Английский язык,
автор: pprohorov907
Предмет: Алгебра,
автор: TOPER24