Предмет: Математика,
автор: Morrl
Вищ. Мат. Похідна
y(x)=x arcsin (x/3)+корінь 9-x²
Приложения:
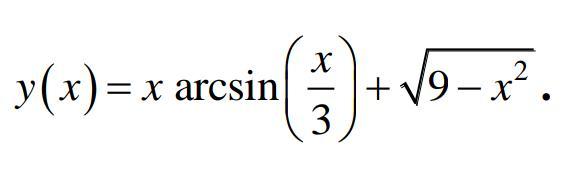
Ответы
Автор ответа:
0
Ответ:
Найти производную функции .
Формулы : .
Правило : .
Приложения:
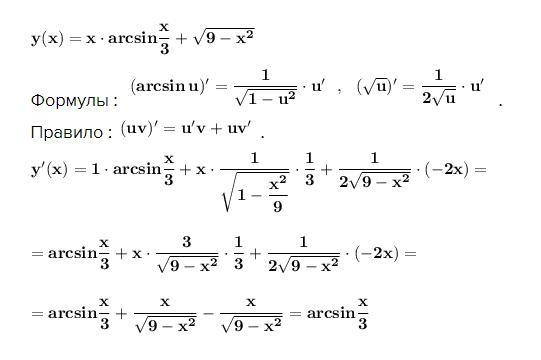
Похожие вопросы
Предмет: Математика,
автор: elnurmuhamedin67
Предмет: Геометрия,
автор: nazarslobodan74
Предмет: Английский язык,
автор: nuraiymnurtaza
Предмет: Химия,
автор: swgav01
Предмет: Музыка,
автор: Аноним