Question

Одна з діагоналей паралелограма
перпендикулярна до його сторони.
Знайдіть більшу сторону
паралелограма, якщо його
діагоналі дорівнюють 12 см і
20 см.

Answer 1

Ответ:

Большая сторона параллелограмма равна 4√13 см.

Объяснение:

Одна из диагоналей параллелограмма перпендикулярна стороне параллелограмма. Найдите большую сторону параллелограмма, если его диагонали равны 12 см и 20 см.

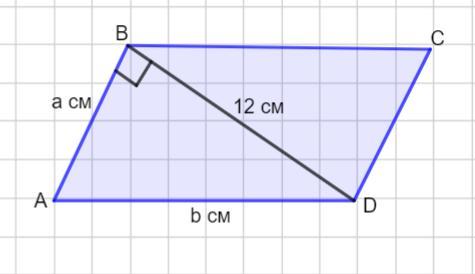
Пусть дан параллелограмм АВСD

Диагональ BD ⊥ AB .

Пусть  АВ =а см , а АD = b см. Рассмотрим  Δ АВD  - прямоугольный и воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Составим уравнение:

$b^{2} - a^{2} =12^{2} ;\\b^{2} - a^{2} =144$

Вторая диагональ параллелограмма равна 20см. Воспользуемся свойством: сумма квадратов диагоналей параллелограмма равна сумме квадратов  его сторон.

Тогда

$2\cdot( a^{2} +b^{2} ) =12^{2} +20^{2} ;\\2\cdot( a^{2} +b^{2} ) =144+400;\\2\cdot( a^{2} +b^{2} ) =544|:2\\a^{2} +b^{2} =272;\\b^{2} +a^{2} =272$

Тогда составим и решим систему уравнений

$\left \{\begin{array}{l} b^{2} -a^{2} = 144, \\ b^{2} +a^{2} = 272; \end{array} \right.\Leftrightarrow \left \{\begin{array}{l} 2b^{2} = 416, \\ b^{2} +a^{2} = 272; \end{array} \right.\Leftrightarrow\left \{\begin{array}{l} b^{2} = 208, \\ 208 +a^{2} = 272; \end{array} \right.\Leftrightarrow\left \{\begin{array}{l} b^{2} = 208, \\ a^{2} = 64 \end{array} \right.$

Так как стороны параллелограмма определяются положительным числом , то

$b= \sqrt{208 } =\sqrt{16\cdot 13} =4\sqrt{13}$ см

$a= \sqrt{64} =8$ см.

Тогда большая сторона параллелограмма равна 4√13 см.

#SPJ1