Предмет: Алгебра,
автор: tortik38601
Периметр прямокутної клумби 28 м. Довжина доріжки, що прокладена по її діагоналі становить 10 м. Якою є площа цієї клумби?
Відповідь: Сторони клумби дорівнюють ... м та ... м. Площа ... м2
Ответы
Автор ответа:
1
Ответ:
Стороны клумбы равны 8 м и 6 м.
Площадь клумбы равна 48 м².
Объяснение:
Периметр прямоугольной клумбы 28 м. Длина дорожки, проложенной по ее диагонали составляет 10 м. Какой является площадь этой клумбы?
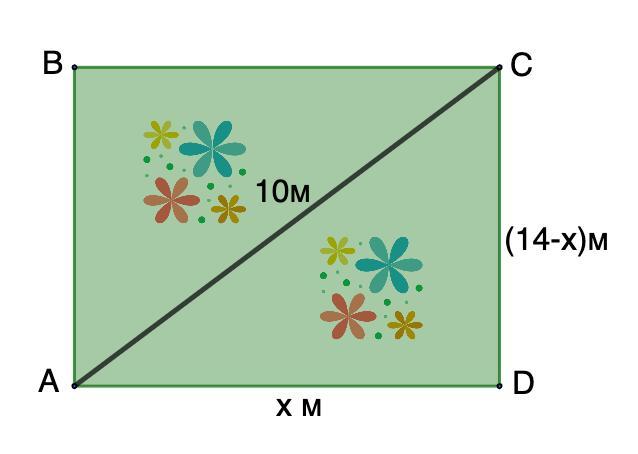
Дано: ABCD - прямоугольник;
Р(ABCD) = 28 м;
АС = 10 м - диагональ.
Найти: S(ABCD)
Решение:
- Периметр прямоугольника равен удвоенной сумме соседних сторон.
P(ABCD) = 2 (AD + DC)
28 = 2 (AD + DC) |:2
AD + DC = 14
Пусть АD = х м ⇒ DC = (14 - x) м
Рассмотрим ΔACD - прямоугольный.
По теореме Пифагора:
AD² + DC² = AC²
x² + (14 - x)^2 = 100
x² + 196 - 28x + x² - 100 = 0
2x² - 28x + 96 = 0 |:2
x² - 14x + 48 = 0
D = 196 - 92 = 4 ⇒ √D = 2
Стороны клумбы равны 8 м и 6 м.
Найдем площадь клумбы.
- Площадь прямоугольника равна произведению соседних сторон.
S(ABCD) = 8 · 6 = 48 (м²)
Площадь клумбы равна 48 м².
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kanaevalikhan
Предмет: Литература,
автор: matgy00
Предмет: Физика,
автор: Palevivid
Предмет: Українська мова,
автор: valeria2464
Предмет: Математика,
автор: 1999fedo