Три кола, радіуси яких дорівнюють 12см, 14см і 16 см, попарно
дотикаються. Визначити площу трикутника, вершини якого лежать
у центрах цих кіл.
Ответы
Ответ:
Площа трикутника дорівнює 336 см²
Объяснение:
Три кола, радіуси яких дорівнюють 12см, 14см і 16 см, попарно
дотикаються. Визначити площу трикутника, вершини якого лежать
у центрах цих кіл.
Розв'язок:
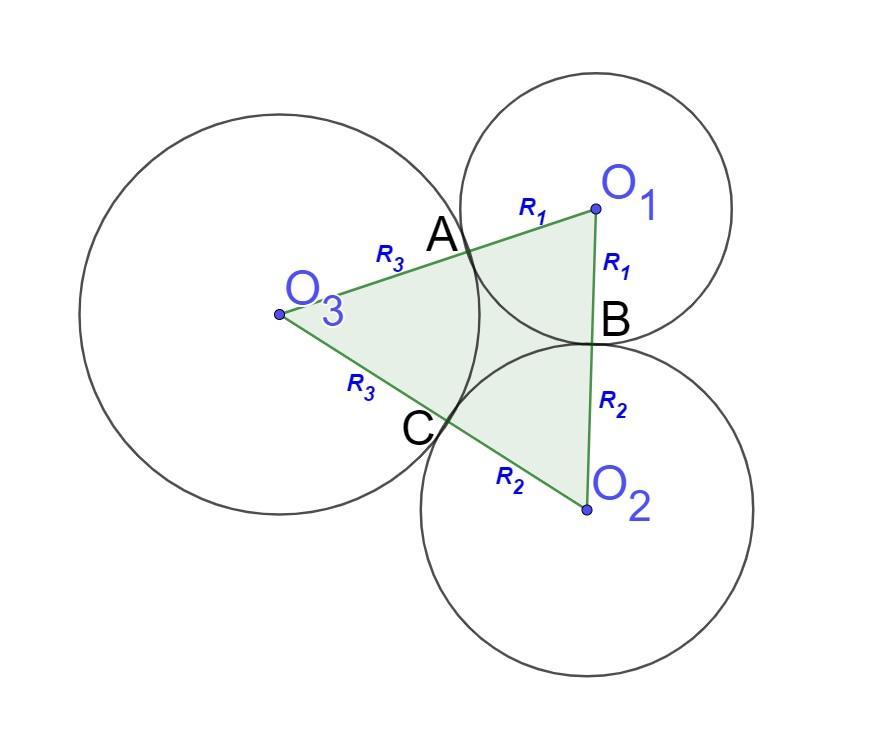
За умовою маємо три кола з центрами, відповідно, у точках O₁, О₂ і О₃ та радіусами R₁=12 см, R₂=14 см, R₃=16 см.
Оскільки три кола попарно дотикаються зовні в точках A, B і C, то відрізки O₁O₂, O₂O₃ і O₁O₃ проходять через ці точки відповідно.
(це випливає із властивості, що дотична в точці дотику перпендикулярна до радіуса кола), де O₁, O₂ і O₃ - центри кіл, що дотикаються зовні.
Знайдемо довжини сторін трикутника:
O₁O₂=О₁В+ВО₂=R₁+R₂=12+14= 26 (см)
O₂O₃= О₂С+СО₃=R₂+R₃=14+16= 30 (см)
O₁O₃=О₁А+АО₃=R₁+R₃=12+16= 28 (см)
Застосуємо формулу Герона, для цього спочатку знайдемо півпериметр ΔО₁О₂О₃:
(см)
За формулою Герона обчислюємо площу ΔО₁О₂О₃:
(см²)
Відповідь: 336 см²
#SPJ1