Предмет: Алгебра,
автор: kimxxx
Даю 30 баллов!!! решите тригонометрическое уравнение.
Приложения:
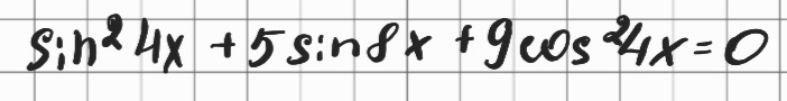
aarr04594:
Розділіть на соs²(4x), далі заміна.
не виходить, якщо спробувати поділити.
Все вийде. Це однорідне рівняння.
Ответы
Автор ответа:
1
Ответ:
x1=(n/4)-
x2=(n-arctg9)/4
Объяснение:
5sin8x+84x+1=0
5sin8x+4(cos(8x)+1)+1=0
5sin8x+4cos8x+5=0
4cos8x+10cos4xsin4x+5=0
-44x+10cos4xsin4x+4
4x+5=0
4x+10cos4xsin4x+9
4x=0
+
+9=0
4x+10tg4x+9=0
Делаем замену: +10t+9=0
За дискриминантом: t1=-1, t2=-9
Обратная замена: tg4x=-1, 4x=n-
, x=(
n/4)-
(1)
tg4x=-9, 4x=n-arctg9, x=(
n-arctg9)/4 (2)
Автор ответа:
0
Відповідь: фото
Пояснення: розв'язання завдання додаю
Приложения:

здравствуйте, помогите пожалуйста с алгеброй, последние задание в моем профиле
Похожие вопросы
Предмет: Литература,
автор: nkvero1
Предмет: Қазақ тiлi,
автор: asel35513
Предмет: Литература,
автор: intergirldn2009
Предмет: Литература,
автор: rriam818
Предмет: Математика,
автор: Аноним