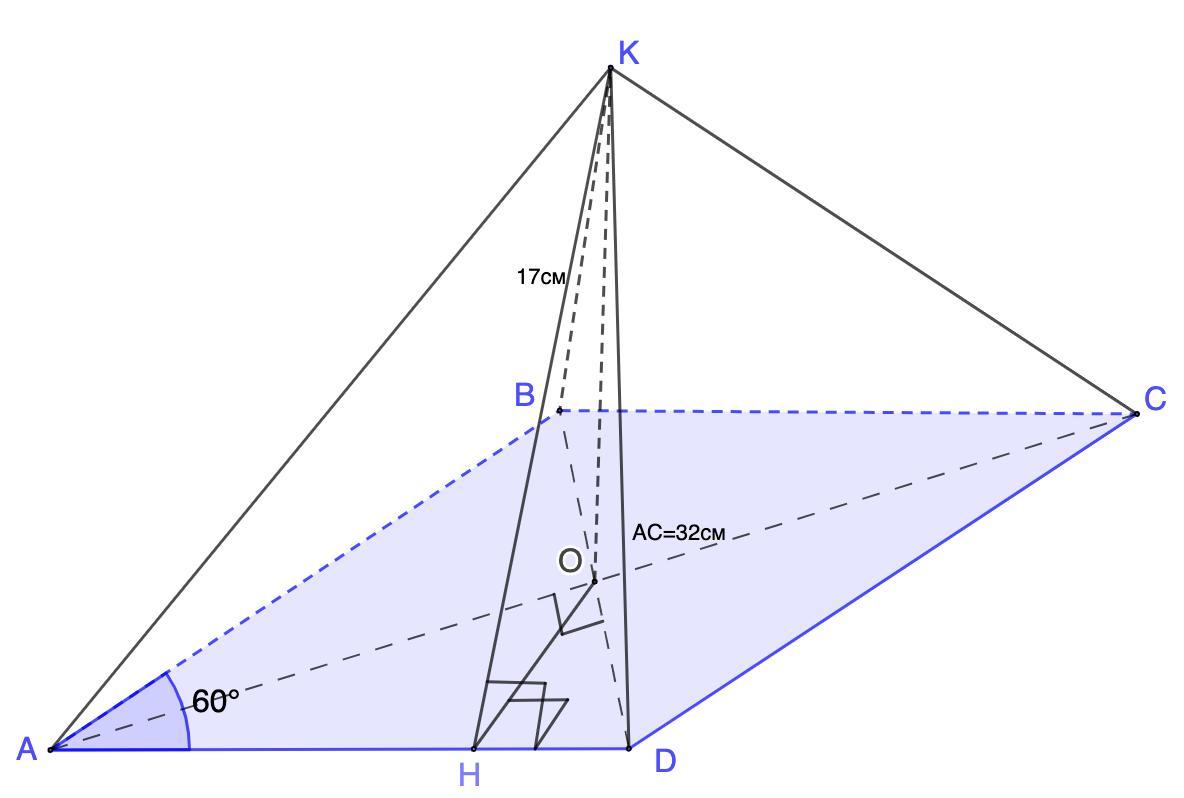
Більша діагональ ромба дорівнює 32 см, а гострий кут 60°. Через точку перетину діагоналей ромба проведено перпендикуляр до його площини. Знайдіть довжину цього перпендикуляра, якщо його другий кінець віддалений від кожної сторони ромба на 17 см.
Ответы
Ответ:
Длина перпендикуляра равна 15 см.
Объяснение:
Большая диагональ ромба равна 32 см, а острый угол 60°. Через точку пересечения диагоналей ромба проведен перпендикуляр к его плоскости. Найдите длину этого перпендикуляра, если его второй конец находится на расстоянии 17 см от каждой стороны ромба.
Дано: ABCD - ромб;
АС = 32 см - диагональ; ∠А = 60°;
ОК ⊥ (ABCD);
Расстояние от К до AD равно 17 см.
Найти: ОК
Решение:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ КН ⊥ AD; КН = 17 см.
Соединим точки Н и О.
КО ⊥ (ABCD) ⇒ HO - проекция КН на (ABCD)
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно самой наклонной, перпендикулярна и ее проекции.
⇒ НО ⊥ AD.
Рассмотрим ΔАОН - прямоугольный.
- Диагонали ромба являются биссектрисами его углов.
∠А = 60° ⇒ ∠ВАО = ∠OAD = 60° : 2 = 30°
- Диагонали ромба точкой пересечения делятся пополам.
⇒ АО = ОС = 32 : 2 = 16 (см)
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ ОН = АО : 2 = 16 : 2 = 8 (см)
Рассмотрим ΔНКО - прямоугольный.
По теореме Пифагора найдем ОК:
ОК² = КН² - ОН² = 289 - 64 = 225 ⇒ ОК = √225 = 15 (см)
Длина перпендикуляра равна 15 см.
#SPJ1