Question

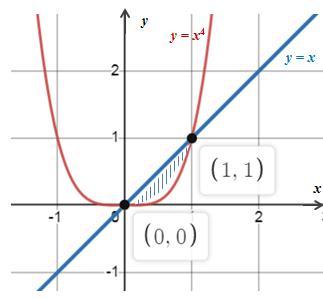
Знайдіть об’єм тіла, утвореного обертанням навколо осі абсцис
фігури, обмеженої лініями
y = x^4 , y = x.

Answer 1

Ответ:

Объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями y = x⁴ и y = x равен $\dfrac{2 \cdot \pi }{9}$ (куб. ед.)

Пошаговое объяснение:

Перевод: Найдите объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями y = x⁴, y = x.

Информация: Объем тела V, образованного вращением вокруг оси абсцисс фигуры y = f(x), a ≤ x ≤ b, определяется по формуле

$V=\pi \cdot \int\limits^b_a {f^2(x)} \, dx .$

Решение. Найдём абсциссу точек пересечения линий y = x⁴ и y = x:

x⁴ = x ⇔ x⁴ - x = 0 ⇔ x·(x³ - 1) = 0 ⇔ x = 0 ∨ x³ - 1 = 0 ⇒ x₁ = 0, x₂ = 1.

Определили границу интегрирования: 0 ≤ x ≤ 1.

Чтобы найти объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями y = x⁴ и y = x, найдём разницу объёмов тел, образованных вращением вокруг оси абсцисс фигуры, ограниченных линиями y = x⁴ и y = x (см. рисунок). То есть

$V=\pi \cdot \int\limits^1_0 {x^2} \, dx -\pi \cdot \int\limits^1_0 {(x^4)^2} \, dx =\pi \cdot \int\limits^1_0 {x^2} \, dx -\pi \cdot \int\limits^1_0 {x^8} \, dx =\\\\=\pi \cdot \dfrac{x^3}{3} |_0^1 -\pi \cdot \dfrac{x^9}{9} |_0^1=\pi \cdot \dfrac{1}{3}-\pi \cdot \dfrac{1}{9}=\pi \cdot (\dfrac{1}{3}-\dfrac{1}{9})=\dfrac{2 \cdot \pi }{9} .$

#SPJ1