Предмет: Алгебра,
автор: Satpad
100 Баллов!!!!
Срочно помогите пж 4 и 5
Приложения:
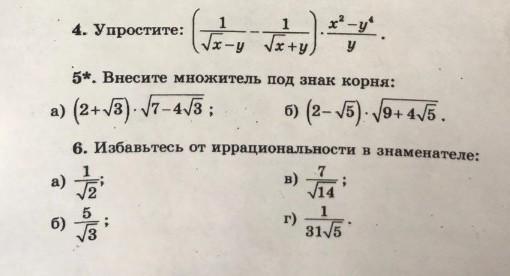
Ответы
Автор ответа:
1
Ответ:
4. на фото
Объяснение:
6.
a) 1/✓2 = ✓2/(✓2)² = ✓2/2
б) 5/✓3 = 5✓3/(✓3)² = 5✓3/9
в) 7/✓14 = 7✓14/(✓14)² = 7✓14/14= ✓14/2
г) 1/31✓5 = ✓5/31(✓5)² = ✓5/155
Приложения:
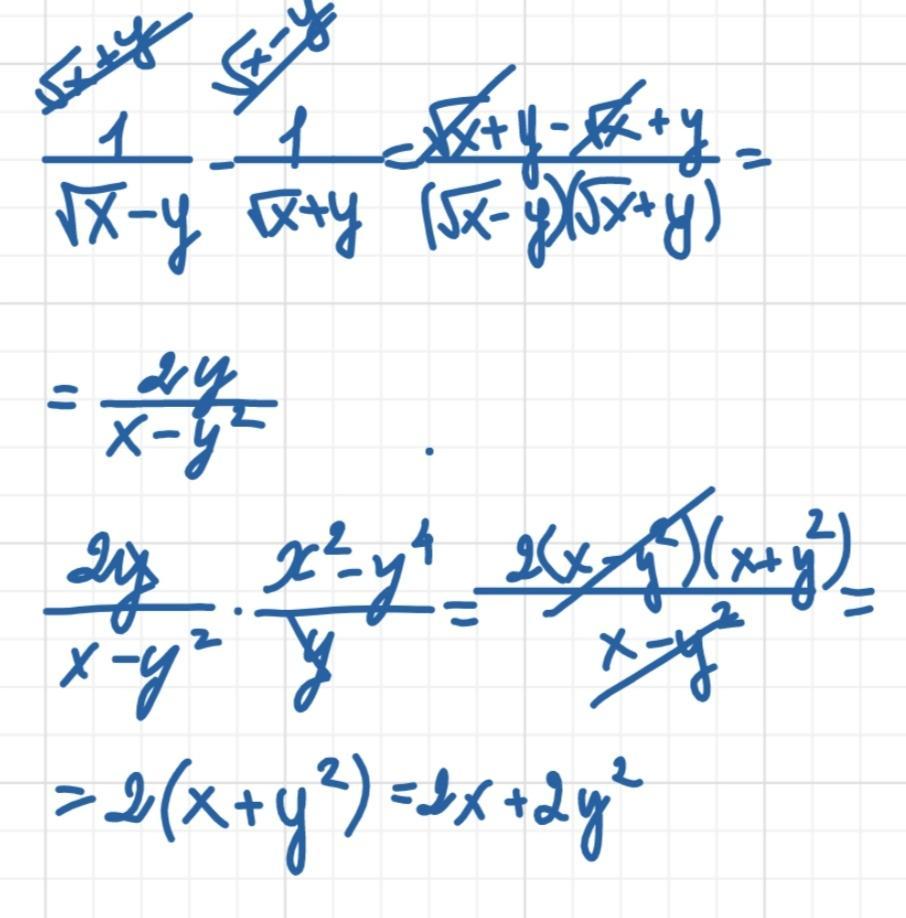
Автор ответа:
0
Ответ:
4) Упростить выражение.
Применяем формулу разности квадратов :
.
5) Внести множитель под знак корня .
Cворачиваем выражение под корнем в квадрат разности или суммы и применяем формулу разности квадратов .
Похожие вопросы
Предмет: Химия,
автор: kolisnicenkobogdaea
Предмет: Английский язык,
автор: innadrevel
Предмет: Математика,
автор: Аноним
Предмет: Музыка,
автор: 666rina555
Предмет: Алгебра,
автор: Аноним