Предмет: Алгебра,
автор: 184mq007
помогите решить пожалуйста
Приложения:
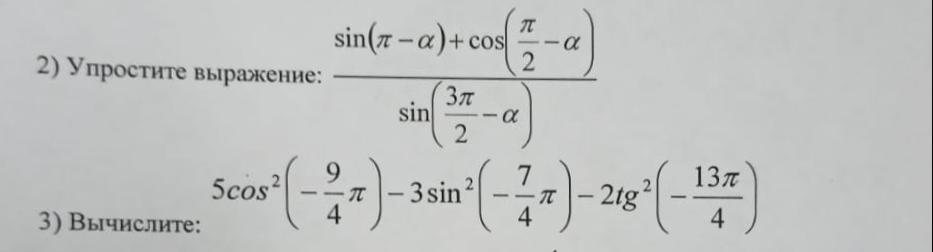
Ответы
Автор ответа:
0
Ответ:
1) Упростить выражение. Применяем формулы приведения .
2) Вычислить. Пользуемся периодичностью тригон. функций .
Похожие вопросы
Предмет: Алгебра,
автор: artem718047
Предмет: Математика,
автор: girlacer36
Предмет: Физика,
автор: Verona14502
Предмет: История,
автор: alisalavrenova0657