Question

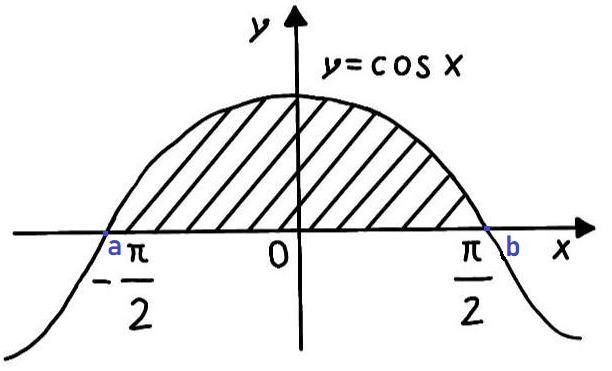
знайдіть площу криволінійної трапеції у=cos x ​

Answer 1

Ответ:

S=2

Пошаговое объяснение:

Разберём задачу постепенно и решим ее:

1. Условие:

$y=cos x\\\\a=-\frac{\pi }{2} \\\\b=\frac{\pi }{2}$

Точки а и b обозначены на рисунке с

низу.

------------------------------------------------------------

Площадь криволинейной трапеции ?

2. Для начала разберем формулу нахождения площади криволинейной трапеции:

$S=\int\limits^b_a{f(x)} \, dx$

Где:

a и b- точки по которым ограничена криволинейная трапеция на оси абсцисс.

f(x)- функция через которую задан рисунок криволинейной трапеции

3.  Теперь прейдём непосредственно к подставке значений и решении интеграла:

 $\int\limits^\frac{\pi }{2} _{-\frac{\pi }{2}} {cosx} \, dx$

1) Для начало мы должны найти  $\int\limits {cosx} \, dx$

То есть мы должны найти первичную функцию от cos x.

Для этого взглянем на второй рисунок закрепленный с низу и найдем, то что нам надо:

$\int\limits {cosx} \, dx =sin x$

2) Вычисли выражение подставив в место х точки а и b. Так же стоит учесть, что мы будем отнимать выражения между собой (от менышего большее):

$sin(\frac{\pi }{2} )-sin(-\frac{\pi }{2} )=1-(-1) =2$

То есть S=2

Вот мы и нашли все, что требовалось в задаче)