Question

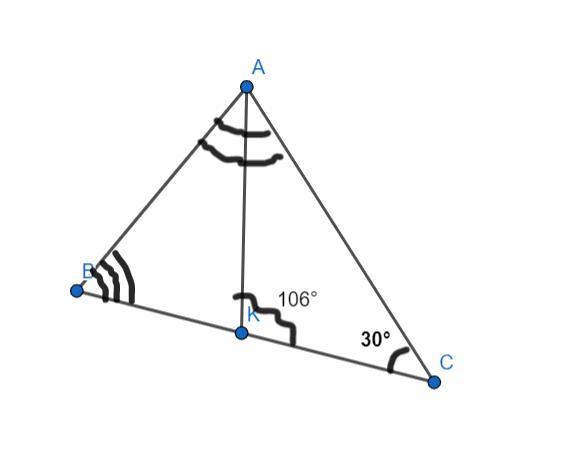
У трикутнику АВС кут С= 30°, АK- бісектриса, ∠АKС = 106°. Знайди ∠ВАС та ∠В.​

Answer 1

Відповідь: ∠ВАС = 88°, ∠В = 62°.

Коротка умова:

Дано: ΔАВС,

∠С= 30°

АK- бісектриса

∠АKС = 106°

Знайти:

∠ВАС - ?

∠В - ?​

Розв'язання:

1. Розглянемо ΔAKC. Згідно теореми про суму кутів трикутника, ∠АKС + ∠KCA + ∠CAK = 106° + 30° + ∠CAK = 180°. Тоді, ∠CAK = 180 - (106 + 30) = 44°.

2. Оскільки, АK- бісектриса, то ∠BAK = ∠CAK = 44°. Тоді, ∠BAC = 44 * 2 = 88°.

3. Згідно теореми про суму кутів трикутника, ∠A + ∠B + ∠C = 88° + ∠B + 30° = 180°. З цього слідує, що ∠B = 180 - (88 + 30) = 62°.

Відповідь: ∠ВАС = 88°, ∠В = 62°.