Предмет: Геометрия,
автор: 009nmmn009
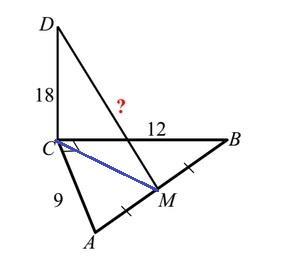
У трикутнику АВС відомо, що кут С дорівнює 90º, АС=9, ВС=12, точка М – середина ВА. Пряма DC перпендикулярна до площини АВС, DC=18. Знайдіть DM.
Ответы
Автор ответа:
3
Ответ:
DM дорівнює 19,5 од.
Объяснение:
У трикутнику АВС відомо, що кут С дорівнює 90º, АС=9, ВС=12, точка М – середина ВА. Пряма DC перпендикулярна до площини АВС, DC=18. Знайдіть DM.
1. У ΔАВС за теоремою Пифагора знайдемо гипотенузу АВ.
АВ²=ВС²+АС²
АВ²=12²+9²=144+81=225
АВ=√225=15 (од)
2. Так як точка М – середина АВ, то СМ - медиана, проведена до гіпотенузи.
- Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.
СМ=1/2·АВ=1/2·15=7,5 (ед)
3. За умовою DC⊥(ABC), тому (за властивістю) вона перпендикулярна до кожної прямої, що належить площині ABC.
СМ ∈ (АВС), тому DC⊥СМ ⇒ΔDCM - прямокутний, ∠DCM=90°.
За теоремою Пифагора знайдемо гипотенузу DM.
DM²=DC²+CM²
DM²=18²+7,5²=324+56,25=380,25
DM=19,5 (од)
Відповідь: 19,5 од
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: dalilzeinalov
Предмет: Химия,
автор: idhd44dojd
Предмет: Математика,
автор: akmarjanraimbekova
Предмет: Українська мова,
автор: faq4ers
Предмет: Математика,
автор: miras0607b