Question

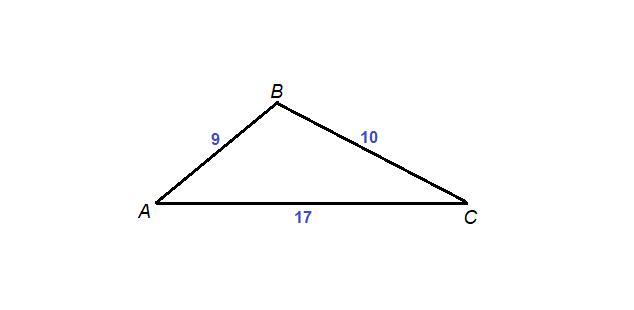
Знайти радіус вписаного та описаного кола для трикутника зі сторонами 9,10, 17 см

Answer 1

Ответ:

r = 2 см

R = 10,625 см²

Объяснение:

АВ = 9 см, ВС = 10 см, АС = 17 см.

Найдем площадь треугольника по формуле Герона:

$S=\sqrt{p(p-AB)(p-BC)(p-AC)}$

Полупериметр треугольника:

$p=\dfrac{AB+BC+AC}{2}=\dfrac{9+10+17}{2}=18$

р = 18 см

$S=\sqrt{18\cdot (18-9)(18-10)(18-17)}$

$S=\sqrt{18\cdot 9\cdot 8\cdot 1}=\sqrt{9\cdot 2\cdot 9\cdot 2\cdot 4}=3\cdot 2\cdot 3\cdot 2=36$

S = 36 см²

Найдем радиус вписанной окружности из формулы:

$S =pr$

$r=\dfrac{S}{p}=\dfrac{36}{18}=2$

r = 2 см

Найдем радиус описанной окружности из формулы:

$S=\dfrac{AB\cdot BC\cdot AC}{4R}$

$R=\dfrac{AB\cdot BC\cdot AC}{4S}=\dfrac{9\cdot 10\cdot 17}{4\cdot 36}=\dfrac{5\cdot 17}{2\cdot 4}=\dfrac{85}{8}=10,625$

R = 10,625 см²