Question

Люди добрые, помогите, пожалуйста, с задачей! Заранее спасибо!
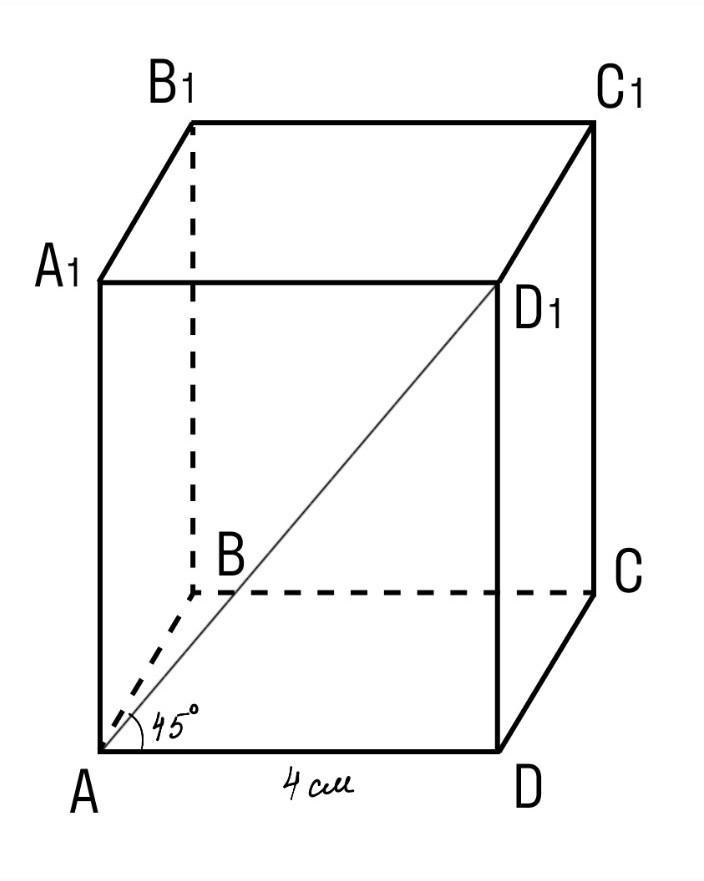
Сторона основания правильной четырехугольной призмы равна 4 см, диагональ боковой грани призмы наклонена к плоскости основания под углом 45°. Найдите: 1) площадь основания; 2) высоту призмы; 3) объем призмы.

Answer 1

Ответ:

1) 16 (см²)

2) 4 (см)

3) 64 (см³)

Объяснение:

Дано:

АВСDA₁B₁C₁D₁ - правильная четырехугольная призма

а$_{osn}$ = AB = 4 см

d = AD₁ - диагональ бок.грани

∠(AD₁;(ABC)) = 45°

Найти:

1) S$_{osn}$

2) h

3) V

Решение:

Так как основание нашей призмы это - квадрат , тогда площадь основания найти легко :

$\displaystyle \boldsymbol{S_{osn} = a^2=4^2=16(cm^2)}$

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость. Таким образом ∠D₁AB = 45°. Высотой призмы называется любое ребро , которое перпендикулярна основаниям. Тогда рассм. прямоугольный ∆D₁AB .

Если один из острых углов прямоугольного треугольника равен 45° , то этот треугольник равнобедренный , следовательно AB = DD₁ = 4 см - это высота призмы. Объем можно найти переумножив площадь основания на высоту:

$\boldsymbol{V = S_{osn} \cdot h = 16 \cdot4 = 64(cm {}^{3} )}$