Question

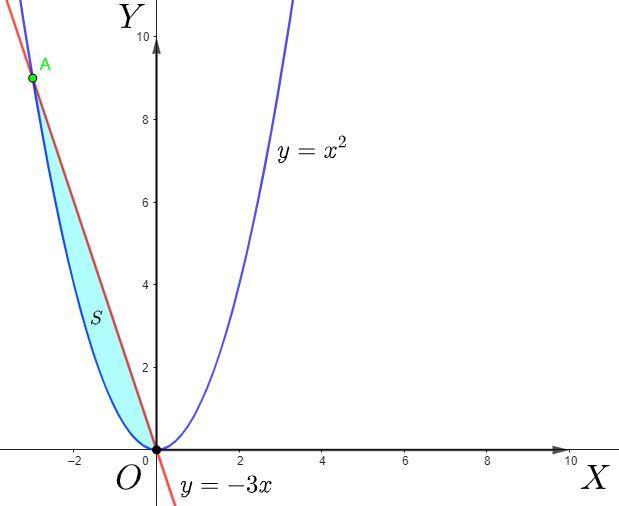
знайдіть площу фігури обмеженої лініями y=x² і y= -3x
​

Answer 1

Ответ:

Площадь фигуры ограниченной линиями равна 4,5 квадратных единиц

Пошаговое объяснение:

Линии ограничивающие фигуру(площадь):

$y =x^{2}$

$y =-3x$

Абсциссы пересечения линий ограничивающих фигуру:

$x^{2} =-3x$

$x^{2} + 3x = 0$

$x(x + 3) = 0$

$x_{1} = 0$ или $x_{2} =-3$

Так как график $y =-3x$ находится над графиком $y =x^{2}$ и абсциссы пересечения данных графиков есть точки 0 и -3, то согласно геометрическому смыслу определенного интеграла, площадь фигуры ограниченной линиями есть:

$\displaystyle S = \int\limits^{0}_{-3} {(-3x - x^{2} )} \, dx = -\int\limits^{0}_{-3} {(3x + x^{2} )} \, dx = -\Bigg(\int\limits^{0}_{-3} {3x} \, dx+\int\limits^{0}_{-3} { x^{2}} \, dx \Bigg)=$

$\displaystyle= -\Bigg(3\int\limits^{0}_{-3} {x} \, dx+\int\limits^{0}_{-3} { x^{2}} \, dx \Bigg)= - \Bigg (3 \cdot \dfrac{x^{2} }{2} \bigg |_{-3}^{0} + \dfrac{x^{3}}{3} \bigg |_{-3}^{0} \Bigg )=$

$\displaystyle = - \bigg (\frac{3}{2}\bigg(0^{2} - (-3)^{2}) + \frac{1}{3} \bigg(0^{3} - (-3)^{3} \bigg) \bigg) = - \bigg (\frac{3}{2}\bigg(0 - 9) + \frac{1}{3} \bigg(0 +27\bigg) \bigg) =$

$\displaystyle = - \bigg (-\frac{9 \cdot 3}{2} + \frac{27}{3} \bigg) = -9 +13,5 = 4,5$ квадратных единиц.