Предмет: Математика,
автор: 95fwcwjshn
Прошу помочь с задачей!!!
Приложения:
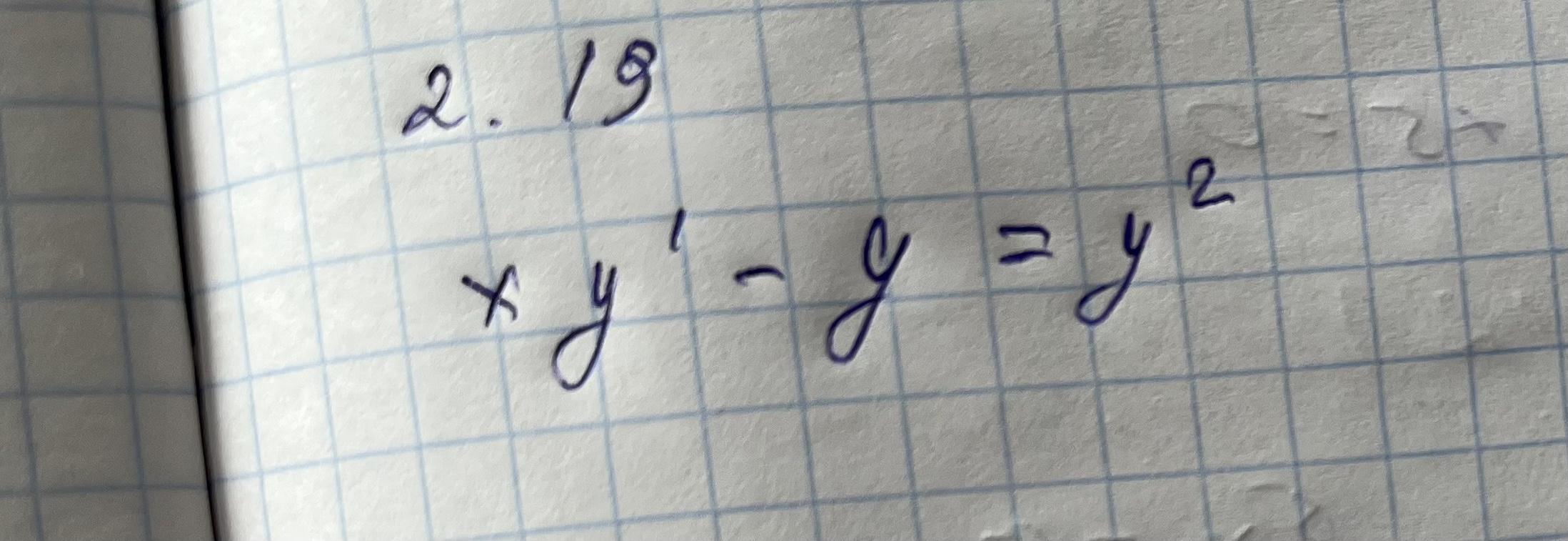
Ответы
Автор ответа:
0
Ответ:
Общий интеграл дифференциального уравнения:
Примечание:
По свойствам интегралов:
Пошаговое объяснение:
- решения дифференциального уравнения
- общий интеграл дифференциального уравнения
Похожие вопросы
Предмет: Русский язык,
автор: Oiljws
Предмет: Русский язык,
автор: Oiljws
Предмет: Математика,
автор: ponbebrjopano000
Предмет: Английский язык,
автор: KONAHINSERGEJ87
Предмет: Математика,
автор: Henk3