Предмет: Геометрия,
автор: ryzhenko2007
допоможіть!!!!!!!!!!!!!
Приложения:
Ответы
Автор ответа:
2
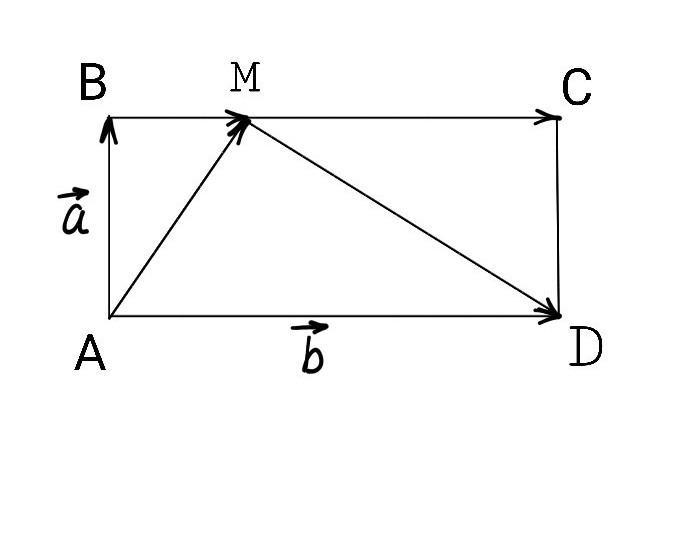
Дано:
ABCD - прямоугольник
Выразить векторы и
через векторы
и
, если M∈BC и MB : MC = 1 : 2
Решение:
Так как АD||ВС и AD=BC , то . По условию МВ:МС = 1:2 , значит , мы можем записать , что МВ = 1/3ВС.
Приступаем. Выразим вектор через векторы
и
. По правилу треугольника(сумма векторов):
Выразим вектор через векторы
и
. Также по правилу треугольника(разность векторов):
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: dmojkisa
Предмет: Математика,
автор: uchihabrr979
Предмет: Алгебра,
автор: monteobebr
Предмет: Математика,
автор: evelinalobastova036