Question

Як найшвидше, будь ласка!!!!
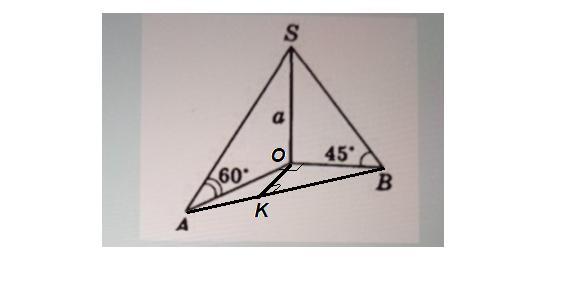
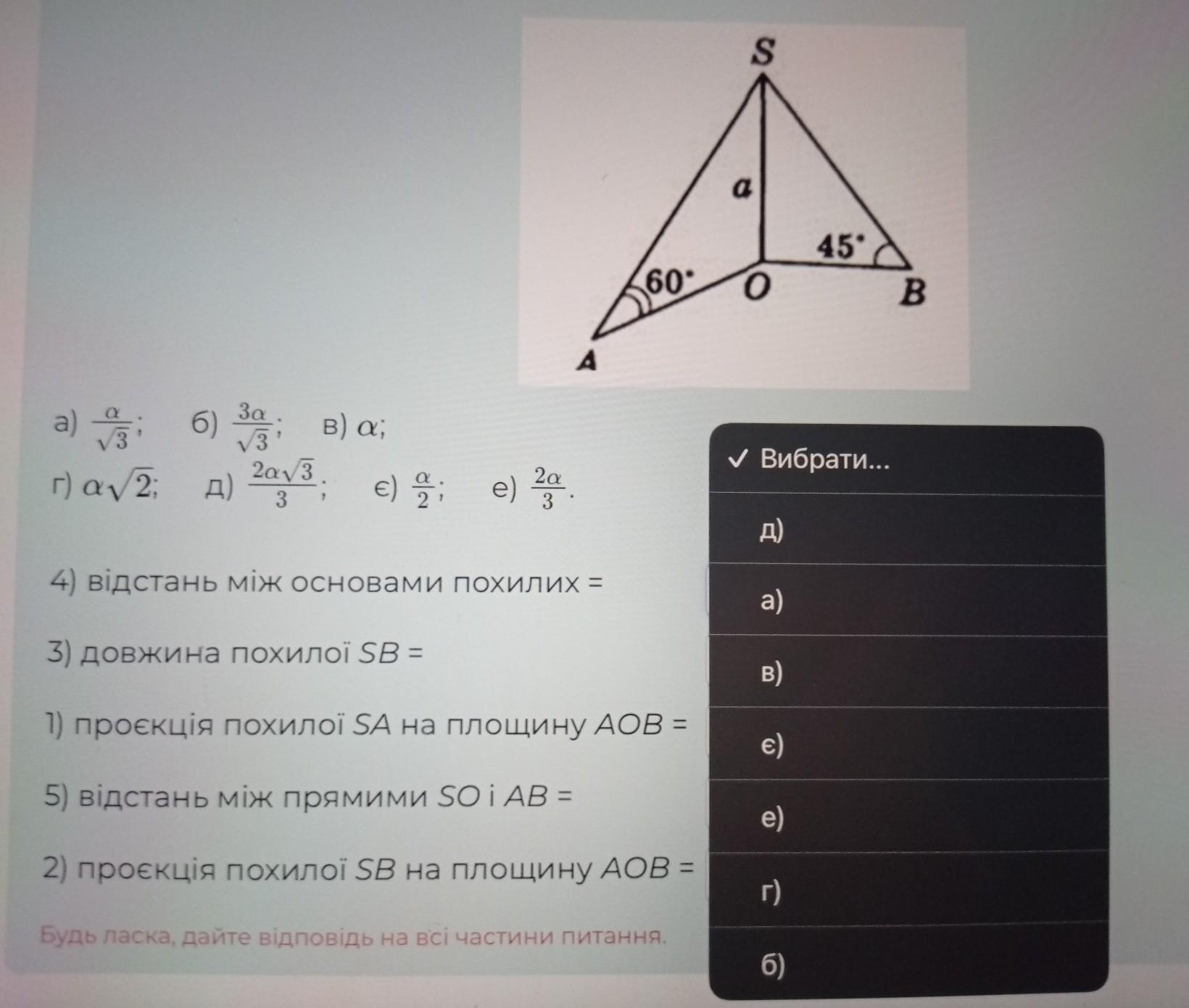
Дано: SO (перпендикулярне)(ABO), SA i SB - похилі, SO = a, кут AOB =90°, кут SAO =60°, кут SBO =45° (рисунок) Користуючись зображенням, встановіть відповідність між відрізками 1) - 5) та їх значеннями а) - е)​

Answer 1

Ответ:

1) а)

2) в)

3) г)

4) д)

5) ∈)

Объяснение:

1) Проекция наклонной SA на плоскость (АОВ) - это отрезок АО.

Из прямоугольного треугольника SAO:

$\dfrac{SO}{AO}=tg\angle SAO$

$AO=\dfrac{SO}{tg\; 60^\circ}=\dfrac{a}{\sqrt{3}}$

Ответ: а)

2) Проекция наклонной SB на плоскость (АОВ) - это отрезок ВО.

Прямоугольный треугольник SOB с острым углом 45° - равнобедренный, значит

BO = SO = a

Ответ: в)

3) Длина наклонной SB.

SB - гипотенуза равнобедренного прямоугольного треугольника, значит

SB = SO√2

SB = a√2

Ответ: г)

4) Расстояние между основаниями наклонных - отрезок АВ.

Из прямоугольного треугольника АОВ по теореме Пифагора:

$AB=\sqrt{AO^2+BO^2}$

$AB=\sqrt{\dfrac{a^2}{3}+a^2}=\sqrt{\dfrac{4a^2}{3}}=\dfrac{2a}{\sqrt{3}}$

Избавимся от иррациональности в знаменателе:

$AB=\dfrac{2a\sqrt{3}}{3}$

Ответ: д)

5) Расстояние между прямыми SO и АВ - это длина общего перпендикуляра к этим прямым.

Проведем ОК⊥АВ.

SO⊥ОК, так как SO перпендикуляр к плоскости (AOB).

ОК - искомое расстояние.

По формуле высоты прямоугольного треугольника:

$OK=\dfrac{AO\cdot BO}{AB}=\dfrac{\dfrac{a}{\sqrt{3}}\cdot a}{\dfrac{2a}{\sqrt{3}}}=\dfrac{a^2}{2a}=\dfrac{a}{2}$

Ответ: ∈)