Предмет: Математика,
автор: SeverS1de
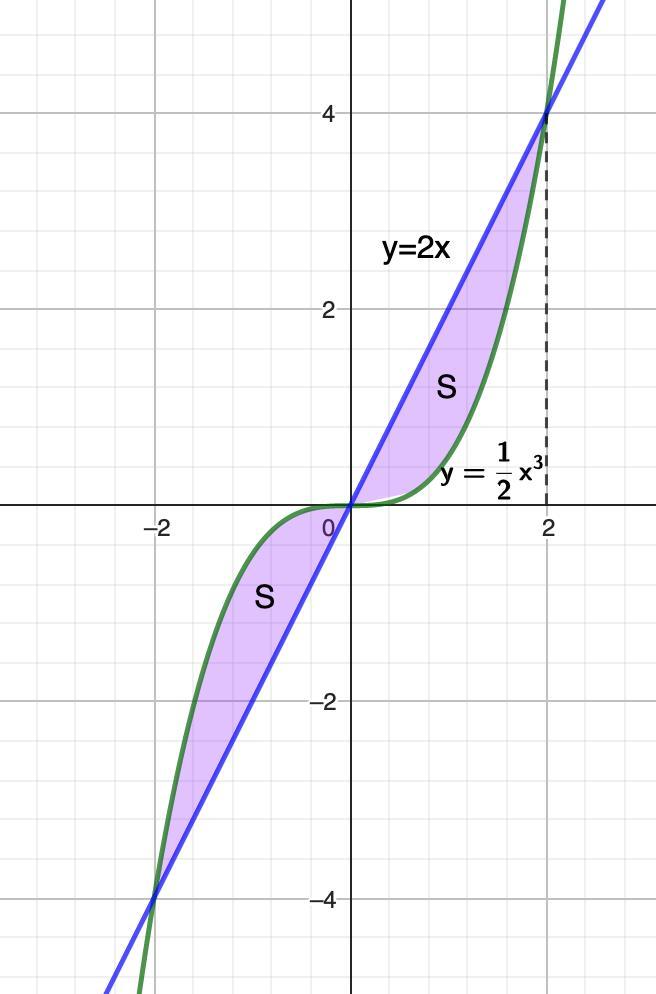
знайдіть площу фігури, обмежену графіком функції

та прямою у=2x
Ответы
Автор ответа:
1
Ответ:
Площадь фигуры, ограниченную графиком функции и прямой y=2x равна 4 ед.².
Пошаговое объяснение:
Найдите площадь фигуры, ограниченную графиком функции и прямой y=2x.
В начале определимся с площадью.
- кубическая парабола.
у = 2х - линейная функция, график - прямая.
Найдем абсциссы точек пересечения этих функций:
Получили две равные площади.
Найдем одну площадь (верхнюю), затем умножим на два.
Формула площади фигуры, ограниченной линиями:
Формула Ньютона - Лейбница:
У нас f₂(x) = 2х (сверху); f₁(x) = (1/2) х³ (снизу); b = 2 (справа); а = 0 (слева)
(ед.²)
⇒ Искомая площадь будет равна 2 · 2 = 4(ед.²)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: DamirUa
Предмет: Информатика,
автор: veronikagolovochenko
Предмет: Информатика,
автор: veronikagolovochenko
Предмет: Геометрия,
автор: mmrr71
Предмет: Математика,
автор: nazymnursultan573829