Предмет: Алгебра,
автор: hapfld
Обчисліть інтеграл, що додається на фото ……….
Приложения:
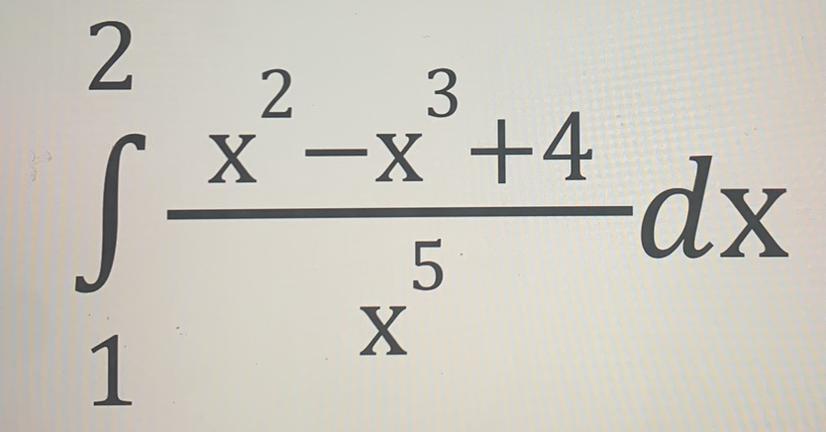
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Алгебра,
автор: hakobjanovgrigori
Предмет: Математика,
автор: dentatarenko2010
Предмет: Математика,
автор: zekasaut
Предмет: Алгебра,
автор: www206
Предмет: Русский язык,
автор: TOP4EG229