Помогите пж, исследование функции с помощью производной и построения графика. Y=2+9x+3x²-x³
Ответы
Ответ:
1. х ∈ R
2. функция не является четной или нечетной.
3. у = 0 ⇒ х₁ ≈ -1,7; х₂ ≈ 4,9; х₃ ≈ -0,2;
х = 0 ⇒ у = 2
4. Функция непрерывна, не периодична, асимптот нет.
5. Функция возрастает на промежутке: [-1; 3]
Функция убывает на промежутках: (-∞; -1]; [3; +∞)
x min = -1; x max = 3
6. Функция вогнута на промежутке: (-∞; 1]
Функция выпукла на промежутке: [1; +∞)
х = 1 - точка перегиба
Пошаговое объяснение:
Исследование функции с помощью производной и построения графика. у = 2 + 9x + 3x² - x³
Дана функция: у = -х³ + 3х² + 9х + 2
1. Область определения функции:
х ∈ R
2. Четность, нечетность.
- Если f(-x) = f(x), то функция четная, если f(-x) = -f(x) - нечетная
у(-х) = -(-х)³ +3(-х)²+9(-х)+2 = х³ + 3х² - 9х + 2
у(-х) ≠ у(х) ≠ -у(х) ⇒ функция не является четной или нечетной.
3. Пересечения с осями.
1) с осью Ох ⇒ у = 0
-х³ + 3х² + 9х + 2 = 0
х₁ ≈ -1,7; х₂ ≈ 4,9; х₃ ≈ -0,2
Уравнение решено с помощью онлайн калькулятора.
2) с осью Оу ⇒ х = 0
у(0) = 2
4. Функция непрерывна, не периодична, асимптот нет.
5. Возрастание, убывание, экстремумы.
Найдем производную, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки производной на промежутках.
у' = -3x² + 6x + 9 = -3(x² - 2x - 3)
y' = 0 ⇒ -3(x² - 2x - 3) = 0
D = 4 +12 = 16; √D = 4
- Если "+" - функция возрастает, если "-" - функция убывает.
Функция возрастает на промежутке: [-1; 3]
Функция убывает на промежутках: (-∞; -1]; [3; +∞)
- Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.
⇒ x min = -1; x max = 3
y(-1) = 1 + 3 - 9 + 2 = -3; y(3) = -27 + 27 +27 + 2 = 29
6. Выпуклость, вогнутость.
Найдем производную второго порядка, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки второй производной на промежутках.
y'' = (-3x² + 6x + 9 )'= -6x + 6
6(1 - x) = 0
x = 1
- Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.
Функция вогнута на промежутке: (-∞; 1]
Функция выпукла на промежутке: [1; +∞)
х = 1 - точка перегиба
у(1) = -1 + 3 + 9 + 2 = 13
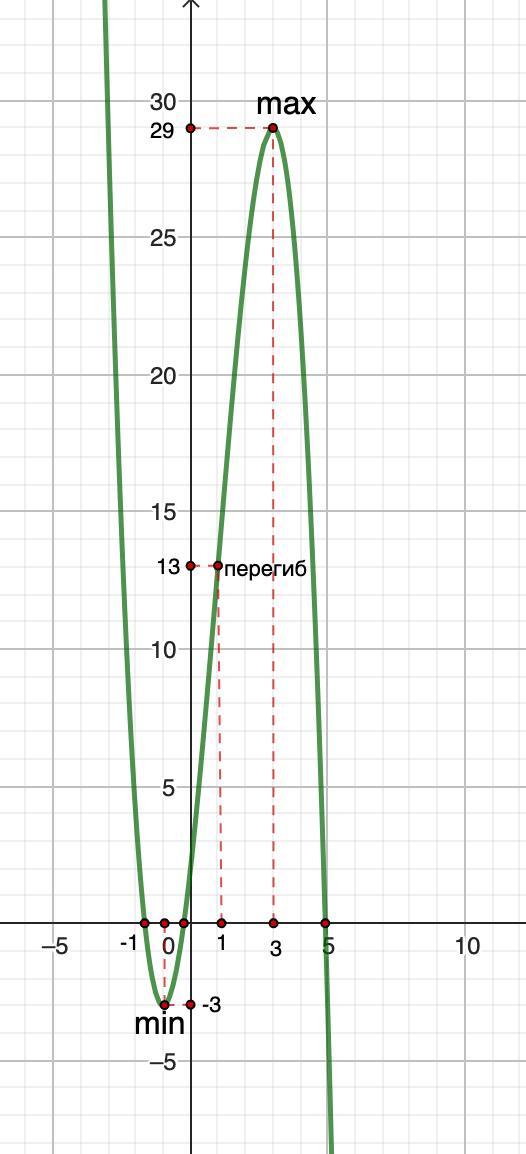
Строим график.